Page 213 - Introduction to Mineral Exploration

196 C.J. MOON & M.K.G. WHATELEY

55,000

50,000

45,000
5
km
N
250,000 255,000 260,000 265,000 270,000 275,000 280,000

Legend Probability
0.03–0.10
Prospect 0.00
0.11–0.40
Coast
0.01–0.02
0.41–0.52
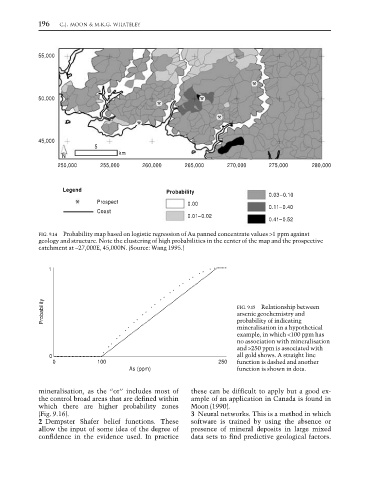
FIG. 9.14 Probability map based on logistic regression of Au panned concentrate values >1 ppm against
geology and structure. Note the clustering of high probabilities in the center of the map and the prospective
catchment at ~27,000E, 45,000N. (Source: Wang 1995.)

1

Probability FIG. 9.15 Relationship between
arsenic geochemistry and
probability of indicating
mineralisation in a hypothetical
example, in which <100 ppm has
no association with mineralisation
and >250 ppm is associated with
0 all gold shows. A straight line
0 100 250 function is dashed and another
As (ppm) function is shown in dots.

mineralisation, as the “or” includes most of these can be difficult to apply but a good ex-
the control broad areas that are defined within ample of an application in Canada is found in
which there are higher probability zones Moon (1990).
(Fig. 9.16). 3 Neural networks. This is a method in which
2 Dempster Shafer belief functions. These software is trained by using the absence or
allow the input of some idea of the degree of presence of mineral deposits in large mixed
confidence in the evidence used. In practice data sets to find predictive geological factors.