Page 77 - MATLAB Recipes for Earth Sciences

4.3 Classical Linear Regression Analysis and Prediction 69

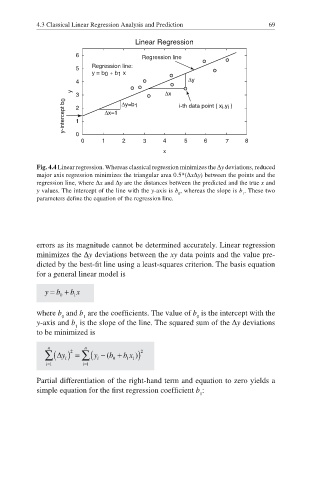
Linear Regression
6 Regression line
Regression line:
5
y = b 0 + b 1 x
4 ∆y
y ∆x
3 ∆y=b 1
y-intercept b 0 2 1 ∆x=1 i-th data point ( x i ,y i )

0
0 1 2 3 4 5 6 7 8
x

Fig. 4.4 Linear regression. Whereas classical regression minimizes the ¨y deviations, reduced
major axis regression minimizes the triangular area 0.5*(¨x¨y) between the points and the
regression line, where ¨x and ¨y are the distances between the predicted and the true x and
y values. The intercept of the line with the y-axis is b , whereas the slope is b . These two
0 1
parameters define the equation of the regression line.

errors as its magnitude cannot be determined accurately. Linear regression
minimizes the ¨y deviations between the xy data points and the value pre-
dicted by the best-fit line using a least-squares criterion. The basis equation

for a general linear model is

where b and b are the coeffi cients. The value of b is the intercept with the
0 1 0
y-axis and b is the slope of the line. The squared sum of the ¨y deviations
1
to be minimized is

Partial differentiation of the right-hand term and equation to zero yields a
simple equation for the first regression coeffi cient b :

1