Page 113 - Marks Calculation for Machine Design

P1: Sanjay
January 4, 2005
Brown˙C02
Brown.cls
M
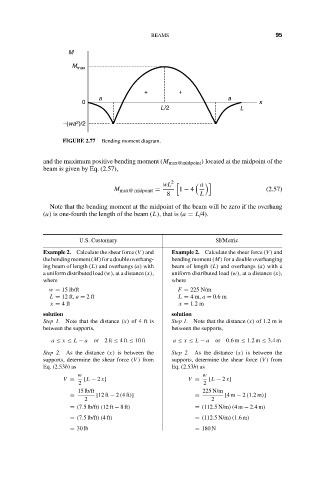
M max 16:18 BEAMS 95
+ +
a a
0 x
L/2 L
–(wa 2 )/2

FIGURE 2.77 Bending moment diagram.

and the maximum positive bending moment (M max@midpoint ) located at the midpoint of the
beam is given by Eq. (2.57),
wL 2
a
M max@ midpoint = 1 − 4 (2.57)
8 L
Note that the bending moment at the midpoint of the beam will be zero if the overhang
(a) is one-fourth the length of the beam (L), that is (a = L/4).

U.S. Customary SI/Metric
Example 2. Calculate the shear force (V ) and Example 2. Calculate the shear force (V ) and
thebendingmoment(M)foradoubleoverhang- bending moment (M) for a double overhanging
ing beam of length (L) and overhangs (a) with beam of length (L) and overhangs (a) with a
a uniform distributed load (w), at a distance (x), uniform distributed load (w), at a distance (x),
where where
w = 15 lb/ft F = 225 N/m
L = 12 ft, a = 2ft L = 4m, a = 0.6 m
x = 4ft x = 1.2 m
solution solution
Step 1. Note that the distance (x) of4ftis Step 1. Note that the distance (x) of 1.2 m is
between the supports, between the supports,
a ≤ x ≤ L − a or 2 ft ≤ 4ft ≤ 10 ft a ≤ x ≤ L − a or 0.6m ≤ 1.2m ≤ 3.4m
Step 2. As the distance (x) is between the Step 2. As the distance (x) is between the
supports, determine the shear force (V ) from supports, determine the shear force (V ) from
Eq. (2.53b)as Eq. (2.53b)as
w w
V = [L − 2 x] V = [L − 2 x]
2 2
15 lb/ft 225 N/m
= [12 ft − 2 (4ft)] = [4 m − 2 (1.2m)]
2 2
= (7.5 lb/ft)(12 ft − 8ft) = (112.5 N/m)(4m − 2.4m)
= (7.5 lb/ft)(4ft) = (112.5 N/m)(1.6m)
= 30 lb = 180 N