Page 74 - Marks Calculation for Machine Design

P1: Sanjay
January 4, 2005
Brown˙C02
Brown.cls
56
U.S. Customary 16:18 STRENGTH OF MACHINES SI/Metric
Step 2. From Fig. 2.31 calculate the roller Step 2. From Fig. 2.31 calculate the roller
reaction (B y ) as reaction (B y ) as
wL (400 lb/ft)(15 ft) wL (6,000 N/m)(5m)
B y = = B y = =
2 2 2 2
6,000 lb 30,000 N
= = 3,000 lb = = 15,000 N
2 2
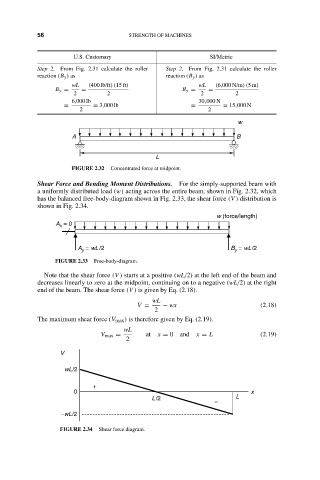
w
A B
L
FIGURE 2.32 Concentrated force at midpoint.
Shear Force and Bending Moment Distributions. For the simply-supported beam with
a uniformly distributed load (w) acting across the entire beam, shown in Fig. 2.32, which
has the balanced free-body-diagram shown in Fig. 2.33, the shear force (V ) distribution is
shown in Fig. 2.34.
w (force/length)
A = 0
x

A = wL /2 B = wL/2
y
y
FIGURE 2.33 Free-body-diagram.
Note that the shear force (V ) starts at a positive (wL/2) at the left end of the beam and
decreases linearly to zero at the midpoint, continuing on to a negative (wL/2) at the right
end of the beam. The shear force (V ) is given by Eq. (2.18).
wL
V = − wx (2.18)
2
The maximum shear force (V max ) is therefore given by Eq. (2.19).
wL
V max = at x = 0 and x = L (2.19)
2
V
wL/2

+
0 x
L/2 L
–
–wL/2

FIGURE 2.34 Shear force diagram.