Page 93 - Marks Calculation for Machine Design

P1: Sanjay
16:18
January 4, 2005
Brown.cls
Brown˙C02
75
BEAMS
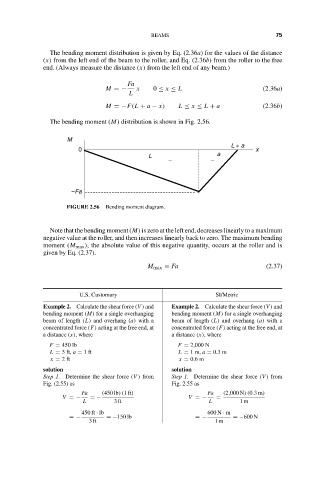
The bending moment distribution is given by Eq. (2.36a) for the values of the distance
(x) from the left end of the beam to the roller, and Eq. (2.36b) from the roller to the free
end. (Always measure the distance (x) from the left end of any beam.)
Fa
M =− x 0 ≤ x ≤ L (2.36a)
L
M =−F(L + a − x) L ≤ x ≤ L + a (2.36b)
The bending moment (M) distribution is shown in Fig. 2.56.
M
L + a
0 x
L a
− −
–Fa

FIGURE 2.56 Bending moment diagram.

Note that the bending moment (M) is zero at the left end, decreases linearly to a maximum
negative value at the roller, and then increases linearly back to zero. The maximum bending
moment (M max ), the absolute value of this negative quantity, occurs at the roller and is
given by Eq. (2.37).
M max = Fa (2.37)

U.S. Customary SI/Metric
Example 2. Calculate the shear force (V ) and Example 2. Calculate the shear force (V ) and
bending moment (M) for a single overhanging bending moment (M) for a single overhanging
beam of length (L) and overhang (a) with a beam of length (L) and overhang (a) with a
concentrated force (F) acting at the free end, at concentrated force (F) acting at the free end, at
a distance (x), where a distance (x), where
F = 450 lb F = 2,000 N
L = 3 ft, a = 1ft L = 1m, a = 0.3 m
x = 2ft x = 0.6 m
solution solution
Step 1. Determine the shear force (V ) from Step 1. Determine the shear force (V ) from
Fig. (2.55) as Fig. 2.55 as
Fa (450 lb)(1ft) Fa (2,000 N)(0.3m)
V =− =− V =− =
L 3ft L 1m
450 ft · lb 600 N · m
=− =−150 lb =− =−600 N
3ft 1m