Page 122 - Master Handbook of Acoustics

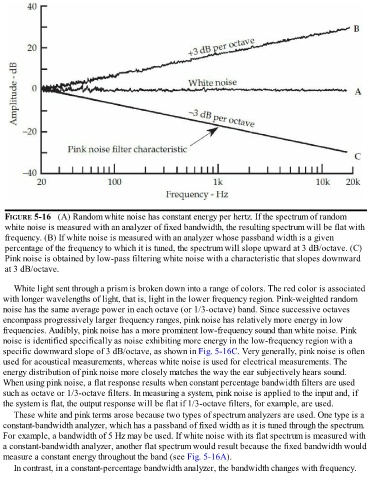
FIGURE 5-16 (A) Random white noise has constant energy per hertz. If the spectrum of random
white noise is measured with an analyzer of fixed bandwidth, the resulting spectrum will be flat with
frequency. (B) If white noise is measured with an analyzer whose passband width is a given
percentage of the frequency to which it is tuned, the spectrum will slope upward at 3 dB/octave. (C)

Pink noise is obtained by low-pass filtering white noise with a characteristic that slopes downward
at 3 dB/octave.

White light sent through a prism is broken down into a range of colors. The red color is associated
with longer wavelengths of light, that is, light in the lower frequency region. Pink-weighted random
noise has the same average power in each octave (or 1/3-octave) band. Since successive octaves
encompass progressively larger frequency ranges, pink noise has relatively more energy in low
frequencies. Audibly, pink noise has a more prominent low-frequency sound than white noise. Pink

noise is identified specifically as noise exhibiting more energy in the low-frequency region with a
specific downward slope of 3 dB/octave, as shown in Fig. 5-16C. Very generally, pink noise is often
used for acoustical measurements, whereas white noise is used for electrical measurements. The
energy distribution of pink noise more closely matches the way the ear subjectively hears sound.
When using pink noise, a flat response results when constant percentage bandwidth filters are used
such as octave or 1/3-octave filters. In measuring a system, pink noise is applied to the input and, if
the system is flat, the output response will be flat if 1/3-octave filters, for example, are used.

These white and pink terms arose because two types of spectrum analyzers are used. One type is a
constant-bandwidth analyzer, which has a passband of fixed width as it is tuned through the spectrum.
For example, a bandwidth of 5 Hz may be used. If white noise with its flat spectrum is measured with
a constant-bandwidth analyzer, another flat spectrum would result because the fixed bandwidth would

measure a constant energy throughout the band (see Fig. 5-16A).
In contrast, in a constant-percentage bandwidth analyzer, the bandwidth changes with frequency.