Page 175 - Materials Science and Engineering An Introduction

5.4 Fick’s Second Law—Nonsteady-State Diffusion • 147

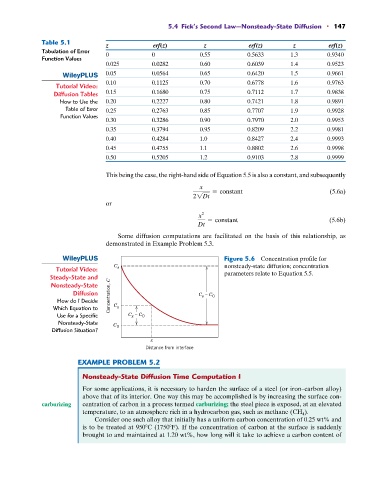
Table 5.1
z erf(z) z erf(z) z erf(z)
Tabulation of Error 0 0 0.55 0.5633 1.3 0.9340
Function Values
0.025 0.0282 0.60 0.6039 1.4 0.9523
0.05 0.0564 0.65 0.6420 1.5 0.9661
0.10 0.1125 0.70 0.6778 1.6 0.9763
Tutorial Video:
Diffusion Tables 0.15 0.1680 0.75 0.7112 1.7 0.9838
How to Use the 0.20 0.2227 0.80 0.7421 1.8 0.9891
Table of Error 0.25 0.2763 0.85 0.7707 1.9 0.9928
Function Values
0.30 0.3286 0.90 0.7970 2.0 0.9953
0.35 0.3794 0.95 0.8209 2.2 0.9981
0.40 0.4284 1.0 0.8427 2.4 0.9993
0.45 0.4755 1.1 0.8802 2.6 0.9998
0.50 0.5205 1.2 0.9103 2.8 0.9999

This being the case, the right-hand side of Equation 5.5 is also a constant, and subsequently

x
= constant (5.6a)
21Dt
or
x 2
= constant (5.6b)
Dt
Some diffusion computations are facilitated on the basis of this relationship, as
demonstrated in Example Problem 5.3.

Figure 5.6 Concentration profile for
C nonsteady-state diffusion; concentration
Tutorial Video: s
Steady-State and parameters relate to Equation 5.5.
Nonsteady-State
Diffusion Concentration, C C – C 0
s
How do I Decide
Which Equation to C x
Use for a Specific C – C 0
x
Nonsteady-State C 0
Diffusion Situation?
x
Distance from interface
EXAMPLE PROBLEM 5.2

Nonsteady-State Diffusion Time Computation I
For some applications, it is necessary to harden the surface of a steel (or iron–carbon alloy)
above that of its interior. One way this may be accomplished is by increasing the surface con-
carburizing centration of carbon in a process termed carburizing; the steel piece is exposed, at an elevated
temperature, to an atmosphere rich in a hydrocarbon gas, such as methane (CH 4 ).
Consider one such alloy that initially has a uniform carbon concentration of 0.25 wt% and
is to be treated at 950 C (1750 F). If the concentration of carbon at the surface is suddenly
brought to and maintained at 1.20 wt%, how long will it take to achieve a carbon content of