Page 180 - Materials Science and Engineering An Introduction

152 • Chapter 5 / Diffusion

EXAMPLE PROBLEM 5.4

Diffusion Coefficient Determination
Using the data in Table 5.2, compute the diffusion coefficient for magnesium in aluminum at
550 C.

Solution
This diffusion coefficient may be determined by applying Equation 5.8; the values of D 0 and Q d
4
2
from Table 5.2 are 1.2 10 m /s and 130 kJ/mol, respectively. Thus,
(130,000 J/mol)
-4 2
D = (1.2 * 10 m /s) expc - # d
(8.31 J/mol K)(550 + 273 K)
2
= 6.7 * 10 -13 m /s

EXAMPLE PROBLEM 5.5

Diffusion Coefficient Activation Energy and Preexponential Calculations
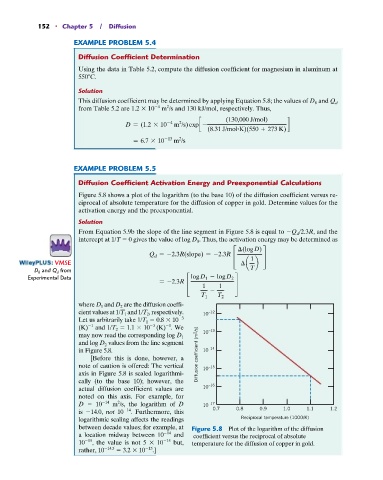
Figure 5.8 shows a plot of the logarithm (to the base 10) of the diffusion coefficient versus re-
ciprocal of absolute temperature for the diffusion of copper in gold. Determine values for the
activation energy and the preexponential.
Solution
From Equation 5.9b the slope of the line segment in Figure 5.8 is equal to Q d /2.3R, and the
intercept at 1/T 0 gives the value of log D 0 . Thus, the activation energy may be determined as
(log D)
Q d = -2.3R(slope) = -2.3R
£ 1 §
: VMSE a b
D 0 and Q d from T
Experimental Data log D 1 - log D 2
= -2.3R
£ 1 1 §
-
T 1 T 2
where D 1 and D 2 are the diffusion coeffi-
cient values at 1/T 1 and 1/T 2 , respectively. 10 –12
Let us arbitrarily take 1/T 1 0.8 10 3
1
1
(K) and 1/T 2 1.1 10 3 (K) . We –13
may now read the corresponding log D 1 10
and log D 2 values from the line segment
in Figure 5.8. 10 –14
[Before this is done, however, a Diffusion coefficient (m 2 /s)
note of caution is offered: The vertical 10 –15
axis in Figure 5.8 is scaled logarithmi-
cally (to the base 10); however, the
actual diffusion coefficient values are 10 –16
noted on this axis. For example, for
D 10 14 m /s, the logarithm of D 10 –17
2
is 14.0, not 10 14 . Furthermore, this 0.7 0.8 0.9 1.0 1.1 1.2
logarithmic scaling affects the readings Reciprocal temperature (1000/K)
between decade values; for example, at Figure 5.8 Plot of the logarithm of the diffusion
a location midway between 10 14 and coefficient versus the reciprocal of absolute
10 15 , the value is not 5 10 15 but, temperature for the diffusion of copper in gold.
rather, 10 14.5 3.2 10 15 .]