Page 121 - Materials Chemistry, Second Edition

108 2 Solid-State Chemistry

a b r(E)
E E

r(E)

Conduction Conduction
E F
Band Band
Valence
Band

E F

Valence
Band

1 - r(E)

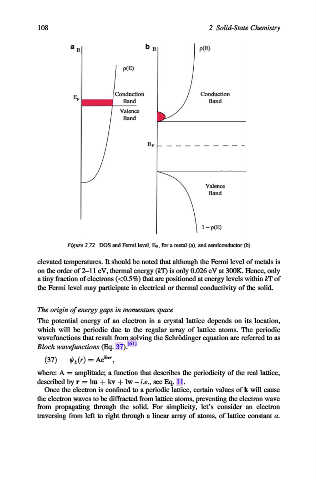
Figure 2.72. DOS and Fermi level, E F , for a metal (a), and semiconductor (b)

elevated temperatures. It should be noted that although the Fermi level of metals is
on the order of 2–11 eV, thermal energy (kT) is only 0.026 eV at 300K. Hence, only
a tiny fraction of electrons (<0.5%) that are positioned at energy levels within kTof
the Fermi level may participate in electrical or thermal conductivity of the solid.

The origin of energy gaps in momentum space
Thepotentialenergyofanelectroninacrystal lattice depends on its location,
which will be periodic due to the regular array of lattice atoms. The periodic
wavefunctions that result from solving the Schr€ odinger equation are referred to as
Bloch wavefunctions (Eq. 37). [61]
ð37Þ c ðrÞ¼ Ae ik r ;
k
where: A ¼ amplitude; a function that describes the periodicity of the real lattice,
described by r ¼ hu þ kv þ lw – i.e., see Eq. 11.
Once the electron is confined to a periodic lattice, certain values of k will cause
the electron waves to be diffracted from lattice atoms, preventing the electron wave
from propagating through the solid. For simplicity, let’s consider an electron
traversing from left to right through a linear array of atoms, of lattice constant a.