Page 195 - Mathematical Models and Algorithms for Power System Optimization

186 Chapter 6

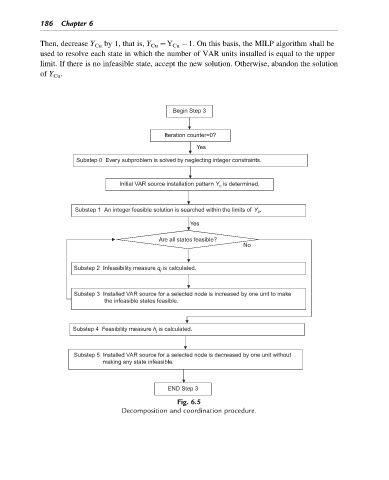
Then, decrease Y Cu by 1, that is, Y Cu ¼Y Cu 1. On this basis, the MILP algorithm shall be
used to resolve each state in which the number of VAR units installed is equal to the upper
limit. If there is no infeasible state, accept the new solution. Otherwise, abandon the solution
of Y Cu .

Begin Step 3

Iteration counter=0?
Yes
Substep 0 Every subproblem is solved by neglecting integer constraints.

Initial VAR source installation pattern Y c is determined.

Substep 1 An integer feasible solution is searched within the limits of Y c .
Yes

Are all states feasible?
No

Substep 2 Infeasibility measure q j is calculated.

Substep 3 Installed VAR source for a selected node is increased by one unit to make
the infeasible states feasible.

Substep 4 Feasibility measure h j is calculated.

Substep 5 Installed VAR source for a selected node is decreased by one unit without
making any state infeasible.

END Step 3
Fig. 6.5

Decomposition and coordination procedure.