Page 200 - Mathematical Models and Algorithms for Power System Optimization

Discrete Optimization for Reactive Power Planning 191

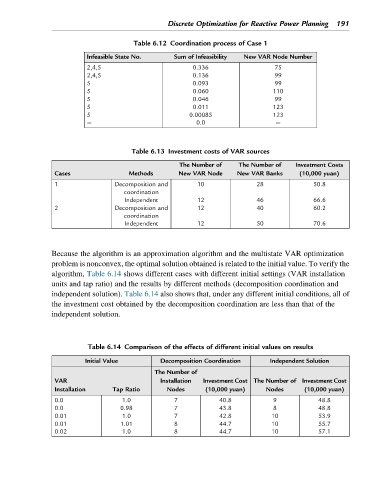
Table 6.12 Coordination process of Case 1
Infeasible State No. Sum of Infeasibility New VAR Node Number

2,4,5 0.336 75
2,4,5 0.136 99
5 0.093 99
5 0.060 110
5 0.046 99
5 0.011 123
5 0.00085 123
— 0.0 —

Table 6.13 Investment costs of VAR sources
The Number of The Number of Investment Costs
Cases Methods New VAR Node New VAR Banks (10,000 yuan)
1 Decomposition and 10 28 50.8
coordination
Independent 12 46 66.6
2 Decomposition and 12 40 60.2
coordination
Independent 12 50 70.6

Because the algorithm is an approximation algorithm and the multistate VAR optimization
problem is nonconvex, the optimal solution obtained is related to the initial value. To verify the
algorithm, Table 6.14 shows different cases with different initial settings (VAR installation
units and tap ratio) and the results by different methods (decomposition coordination and
independent solution). Table 6.14 also shows that, under any different initial conditions, all of
the investment cost obtained by the decomposition coordination are less than that of the
independent solution.

Table 6.14 Comparison of the effects of different initial values on results
Initial Value Decomposition Coordination Independent Solution
The Number of
VAR Installation Investment Cost The Number of Investment Cost
Installation Tap Ratio Nodes (10,000 yuan) Nodes (10,000 yuan)

0.0 1.0 7 40.8 9 48.8
0.0 0.98 7 43.8 8 48.8
0.01 1.0 7 42.8 10 53.9
0.01 1.01 8 44.7 10 55.7
0.02 1.0 8 44.7 10 57.1