Page 201 - Mathematical Models and Algorithms for Power System Optimization

192 Chapter 6

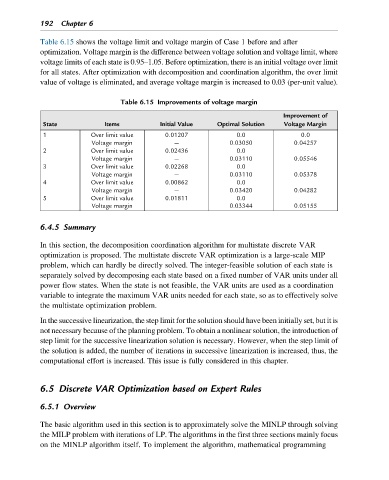
Table 6.15 shows the voltage limit and voltage margin of Case 1 before and after
optimization. Voltage margin is the difference between voltage solution and voltage limit, where
voltage limits of each state is 0.95–1.05. Before optimization, there is an initial voltage over limit
for all states. After optimization with decomposition and coordination algorithm, the over limit
value of voltage is eliminated, and average voltage margin is increased to 0.03 (per-unit value).

Table 6.15 Improvements of voltage margin

Improvement of
State Items Initial Value Optimal Solution Voltage Margin

1 Over limit value 0.01207 0.0 0.0
Voltage margin — 0.03050 0.04257
2 Over limit value 0.02436 0.0
Voltage margin — 0.03110 0.05546
3 Over limit value 0.02268 0.0
Voltage margin — 0.03110 0.05378
4 Over limit value 0.00862 0.0
Voltage margin — 0.03420 0.04282
5 Over limit value 0.01811 0.0
Voltage margin 0.03344 0.05155

6.4.5 Summary

In this section, the decomposition coordination algorithm for multistate discrete VAR
optimization is proposed. The multistate discrete VAR optimization is a large-scale MIP
problem, which can hardly be directly solved. The integer-feasible solution of each state is
separately solved by decomposing each state based on a fixed number of VAR units under all
power flow states. When the state is not feasible, the VAR units are used as a coordination
variable to integrate the maximum VAR units needed for each state, so as to effectively solve
the multistate optimization problem.

In the successive linearization, the step limit for the solution should have been initially set, but it is
not necessary because of the planning problem. To obtain a nonlinear solution, the introduction of
step limit for the successive linearization solution is necessary. However, when the step limit of
the solution is added, the number of iterations in successive linearization is increased, thus, the
computational effort is increased. This issue is fully considered in this chapter.

6.5 Discrete VAR Optimization based on Expert Rules

6.5.1 Overview

The basic algorithm used in this section is to approximately solve the MINLP through solving
the MILP problem with iterations of LP. The algorithms in the first three sections mainly focus
on the MINLP algorithm itself. To implement the algorithm, mathematical programming