Page 141 - Mathematical Techniques of Fractional Order Systems

Exact Solution of Linear Fractional Distributed Order Systems Chapter | 4 129

600

400

200

Im 0

–200
–400

–600

–25 –20 –15 –10
Re
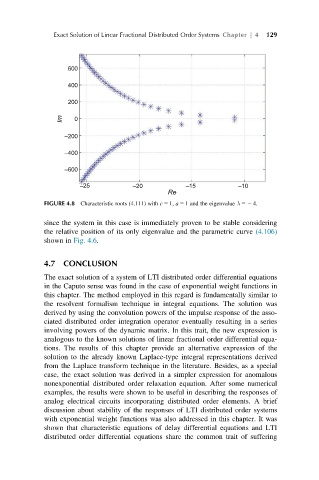
FIGURE 4.8 Characteristic roots (4.111) with c 5 1, a 5 1 and the eigenvalue λ 52 4.

since the system in this case is immediately proven to be stable considering
the relative position of its only eigenvalue and the parametric curve (4.106)
shown in Fig. 4.6.

4.7 CONCLUSION
The exact solution of a system of LTI distributed order differential equations
in the Caputo sense was found in the case of exponential weight functions in
this chapter. The method employed in this regard is fundamentally similar to
the resolvent formalism technique in integral equations. The solution was
derived by using the convolution powers of the impulse response of the asso-
ciated distributed order integration operator eventually resulting in a series
involving powers of the dynamic matrix. In this trait, the new expression is
analogous to the known solutions of linear fractional order differential equa-
tions. The results of this chapter provide an alternative expression of the
solution to the already known Laplace-type integral representations derived
from the Laplace transform technique in the literature. Besides, as a special
case, the exact solution was derived in a simpler expression for anomalous
nonexponential distributed order relaxation equation. After some numerical
examples, the results were shown to be useful in describing the responses of
analog electrical circuits incorporating distributed order elements. A brief
discussion about stability of the responses of LTI distributed order systems
with exponential weight functions was also addressed in this chapter. It was
shown that characteristic equations of delay differential equations and LTI
distributed order differential equations share the common trait of suffering