Page 301 - Mathematical Techniques of Fractional Order Systems

290 Mathematical Techniques of Fractional Order Systems

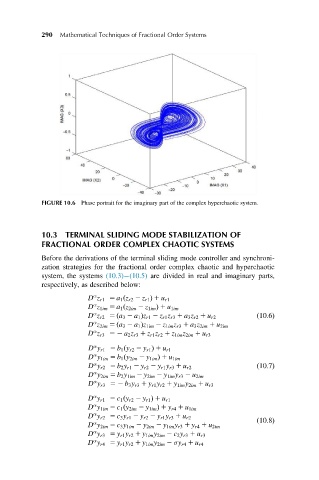
FIGURE 10.6 Phase portrait for the imaginary part of the complex hyperchaotic system.

10.3 TERMINAL SLIDING MODE STABILIZATION OF
FRACTIONAL ORDER COMPLEX CHAOTIC SYSTEMS
Before the derivations of the terminal sliding mode controller and synchroni-
zation strategies for the fractional order complex chaotic and hyperchaotic
system, the systems (10.3) (10.5) are divided in real and imaginary parts,
respectively, as described below:
α
D z r1 5 a 1 ðz r2 2 z r1 Þ 1 u r1
α
D z 1im 5 a 1 ðz 2im 2 z 1im Þ 1 u 1im
α
D z r2 5 ða 3 2 a 1 Þz r1 2 z r1 z r3 1 a 3 z r2 1 u r2 ð10:6Þ
α
D z 2im 5 ða 3 2 a 1 Þz 1im 2 z 1im z r3 1 a 3 z 2im 1 u 2im
α
D z r3 52 a 2 z r3 1 z r1 z r2 1 z 1im z 2im 1 u r3
α
D y r1 5 b 1 ðy r2 2 y r1 Þ 1 u r1
α
D y 1im 5 b 1 ðy 2im 2 y 1im Þ 1 u 1im
α
D y r2 5 b 2 y r1 2 y r2 2 y r1 y r3 1 u r2 ð10:7Þ
α
D y 2im 5 b 2 y 1im 2 y 2im 2 y 1im y r3 2 u 2im
α
D y r3 52 b 3 y r3 1 y r1 y r2 1 y 1im y 2im 1 u r3
α
D y r1 5 c 1 ðy r2 2 y r1 Þ 1 u r1
α
D y 1im 5 c 1 ðy 2im 2 y 1im Þ 1 y r4 1 u 1im
α
D y r2 5 c 3 y r1 2 y r2 2 y r1 y r3 1 u r2
α ð10:8Þ
D y 2im 5 c 3 y 1im 2 y 2im 2 y 1im y r3 1 y r4 1 u 2im
α
D y r3 5 y r1 y r2 1 y 1im y 2im 2 c 2 y r3 1 u r3
α
D y r4 5 y r1 y r2 1 y 1im y 2im 2 σy r4 1 u r4