Page 364 - Mathematical Techniques of Fractional Order Systems

Dual Combination Synchronization Scheme Chapter | 12 355

0.5
0.4
0.1
0 0.3
–0.1 0.2
x 23 (t) –0.2 x 22 (t) 0.1
–0.3
0
–0.4
0.5 –0.1
0.4
0 0.2 –0.2
0
x 22 (t) –0.2 –0.3
–0.5 –0.4 x 21 (t)
–0.3 –0.2 –0.1 0 0.1 0.2
x 21 (t)
(A) (B)
0.1 0.1
0.05 0.05
0 0
–0.05 –0.05
x 23 (t) –0.1 x 23 (t) –0.1
–0.15 –0.15
–0.2 –0.2
–0.25 –0.25
–0.3 –0.3
–0.35 –0.35
–0.3 –0.2 –0.1 0 0.1 0.2 –0.3 –0.2 –0.1 0 0.1 0.2 0.3 0.4 0.5
x 21 (t) x 22 (t)
(C) (D)
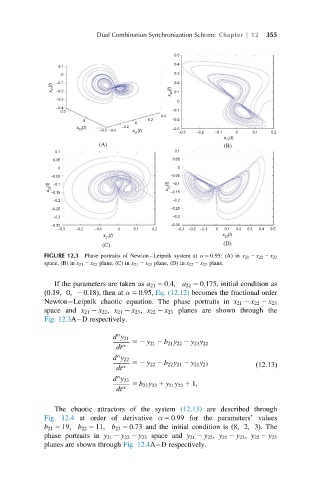
FIGURE 12.3 Phase portraits of Newton Leipnik system at α 5 0:95: (A) in x 21 2 x 22 2 x 23
space, (B) in x 21 2 x 22 plane, (C) in x 21 2 x 23 plane, (D) in x 22 2 x 23 plane.

If the parameters are taken as a 21 5 0:4; a 22 5 0:175, initial condition as
ð0:19; 0; 2 0:18Þ, then at α 5 0:95; Eq. (12.12) becomes the fractional order
Newton Leipnik chaotic equation. The phase portraits in x 21 2 x 22 2 x 23
space and x 21 2 x 22 , x 21 2 x 23 , x 22 2 x 23 planes are shown through the
Fig. 12.3A D respectively.

α
d y 21
dt α 52 y 21 2 b 21 y 22 2 y 23 y 22
α
d y 22
dt α 52 y 22 2 b 22 y 21 2 y 21 y 23 ð12:13Þ
α
d y 23 5 b 23 y 23 1 y 21 y 22 1 1;
dt α

The chaotic attractors of the system (12.13) are described through
Fig. 12.4 at order of derivative α 5 0:99 for the parameters’ values
b 21 5 19; b 22 5 11; b 23 5 0:73 and the initial condition is ð8; 2; 3Þ.The
phase portraits in y 21 2 y 22 2 y 23 space and y 21 2 y 22 , y 21 2 y 23 , y 22 2 y 23
planes are shown through Fig. 12.4A D respectively.