Page 367 - Mathematical Techniques of Fractional Order Systems
P. 367
358 Mathematical Techniques of Fractional Order Systems
2 1
0.5
1
0
y 33 (t) 0 y 34 (t) –0.5
–1 –1
–2 –1.5
5 5
4 4
0 0 2 2 0 0 2 2
0 0 0 0
(
y y
–2
y 32 (t) –2 y 32 (t) t t ) –2
y 32
–2
–5 –4 y 31 (t) –5 –4
y 31 (t)
(A) (B)
1 1
0.5 0.5
0 0
y 34 (t) –0.5 y 34 (t) –0.5
–1 –1
–1.5 –1.5
2 2
1 4 1 5
0 0 2 0 0
y (t) –1 –2 y (t) –1
33 33 –5 y (t)
–2 –4 –2 32
y (t)
31
(C) (D)
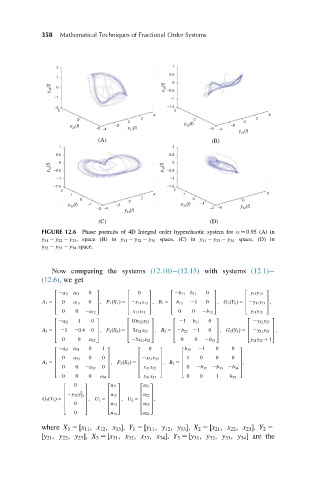
FIGURE 12.6 Phase portraits of 4D Integral order hyperchaotic system for α 5 0:95 (A) in
y 31 2 y 32 2 y 33 , space (B) in y 31 2 y 32 2 y 34 space, (C) in y 31 2 y 33 2 y 34 space, (D) in
y 32 2 y 33 2 y 34 space.
Now comparing the systems (12.10) (12.15) with systems (12.1)
(12.6), we get
2 0 3 2 0 3 2 0 3 2 3
2a 11 a 11 2b 11 b 11 y 12 y 13
6 7 6 7 6 7 6 7
0 0 21 0 7 ;
A 1 5 6 a 13 7 ; F 1 ðX 1 Þ5 6 7 ; B 1 5 6 b 13 7 ; G 1 ðY 1 Þ5 6
4 5 4 2x 11 x 13 5 4 5 4 2y 11 y 13 5
0 0 2a 12 x 11 x 12 0 0 2b 12 y 11 y 12
2 1 0 3 2 3 2 21 0 3 2 3
2a 21 10x 22 x 23 b 21 2y 22 y 23
6 7 6 7 6 7 6 7
21 20:4 21 0 7 ;
A 2 5 6 0 7 ; F 2 ðX 2 Þ5 6 7 ; B 2 5 6 2b 22 7 ; G 2 ðY 2 Þ5 6
4 5 4 5x 21 x 23 5 4 5 4 2y 21 y 23 5
0 0 a 22 25x 21 x 22 0 0 2b 23 y 21 y 22 11
2 0 1 3 2 0 3 2 21 0 0 3
2a 31 a 31 b 31
0 0 1 0 0 0
6 7 6 7 6 7
6 a 33 0 7 6 2x 31 x 33 7 6 7
7 ;
A 3 5 6 7 ; F 3 ðX 3 Þ5 6 7 ; B 3 5 6
0 0 0
6 7 6 7 6 7
4 2a 32 0 5 4 x 31 x 32 5 4 2b 32 2b 33 2b 34 5
0 0 0 a 34 x 31 x 33 0 0 1 b 35
0 u 11 u 21
2 3 2 3 2 3
6 6 7 6 7
2 7
6 2y 32 y 33 7 6 u 12 7 6 u 22 7
7 ;
G 3 ðY 3 Þ5 6 7 ; U 1 5 6 7 ; U 2 5 6
0
6 7 6 7 6 7
4 5 4 u 13 5 4 u 23 5
0 u 14 u 24
where X 1 5 ½x 11 ; x 12 ; x 13 , Y 1 5 ½y 11 ; y 12 ; y 13 , X 2 5 ½x 21 ; x 22 ; x 23 , Y 2 5
½y 21 ; y 22 ; y 23 , X 3 5 ½x 31 ; x 32 ; x 33 ; x 34 , Y 3 5 ½y 31 ; y 32 ; y 33 ; y 34 are the