Page 372 - Mathematical Techniques of Fractional Order Systems

Dual Combination Synchronization Scheme Chapter | 12 363

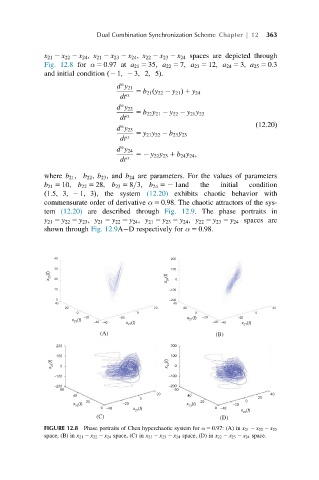
x 21 2 x 22 2 x 24 , x 21 2 x 23 2 x 24 , x 22 2 x 23 2 x 24 spaces are depicted through
Fig. 12.8 for α 5 0:97 at a 21 5 35; a 22 5 7; a 23 5 12; a 24 5 3, a 25 5 0:3
and initial condition ð2 1; 2 3; 2; 5Þ.
α
d y 21
dt α 5 b 21 ðy 22 2 y 21 Þ 1 y 24
α
d y 22
dt α 5 b 22 y 21 2 y 22 2 y 21 y 23
α ð12:20Þ
d y 23
dt α 5 y 21 y 22 2 b 23 y 23
α
d y 24
52 y 22 y 23 1 b 24 y 24 ;
dt α
where b 21 ; b 22 , b 23 , and b 24 are parameters. For the values of parameters
b 21 5 10; b 22 5 28; b 23 5 8=3; b 24 52 1and the initial condition
ð1:5; 3; 2 1; 3Þ, the system (12.20) exhibits chaotic behavior with
commensurate order of derivative α 5 0:98: The chaotic attractors of the sys-
tem (12.20) are described through Fig. 12.9. The phase portraits in
y 21 2 y 22 2 y 23 , y 21 2 y 22 2 y 24 , y 21 2 y 23 2 y 24 , y 22 2 y 23 2 y 24 spaces are
shown through Fig. 12.9A D respectively for α 5 0:98.

40 200
30 100
x 23 (t) 20 x 24 (t) 0

10 –100
0 –200
40 40
20 20 20 20
0 0 0 0
–20 –20 x 21 (t) –20 –20
x 22 (t)
–40 –40 x 21 (t) –40 –40 x 21 (t)
(A) (B)
200 200
100 100
x 23 (t) 0 x 24 (t) 0
–100 –100
–200 –200
60 60
20 40
40 40
0 20
20 20 0
x 23 (t) –20 x 23 (t) –20
0 –40 x 21 (t) 0 –40
x 22 (t)
(C) (D)
FIGURE 12.8 Phase portraits of Chen hyperchaotic system for α 5 0:97: (A) in x 21 2 x 22 2 x 23
space, (B) in x 21 2 x 22 2 x 24 space, (C) in x 21 2 x 23 2 x 24 space, (D) in x 22 2 x 23 2 x 24 space.