Page 454 - Mathematical Techniques of Fractional Order Systems

Applications of Continuous-time Fractional Order Chapter | 14 439

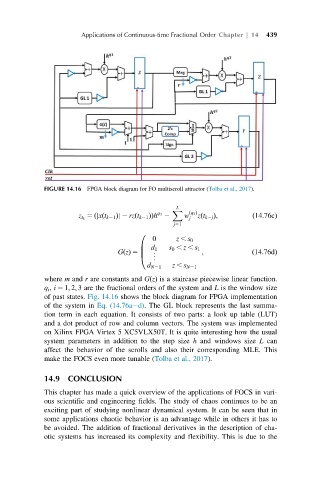
FIGURE 14.16 FPGA block diagram for FO multiscroll attractor (Tolba et al., 2017).

L
X
5 jxðt k21 Þj 2 rzðt k21 ÞÞh 2 w ðq 3 Þ zðt k2j Þ;
q 3
j
z t k ð ð14:76cÞ
j51
0
0 z , s 0
B d 1 s 0 , z , s 1
GðzÞ 5 B ; ð14:76dÞ
^
@
d N21 z , s N21
where m and r are constants and GðzÞ is a staircase piecewise linear function.
q i , i 5 1; 2; 3 are the fractional orders of the system and L is the window size
of past states. Fig. 14.16 shows the block diagram for FPGA implementation
of the system in Eq. (14.76a d). The GL block represents the last summa-
tion term in each equation. It consists of two parts: a look up table (LUT)
and a dot product of row and column vectors. The system was implemented
on Xilinx FPGA Virtex 5 XC5VLX50T. It is quite interesting how the usual
system parameters in addition to the step size h and windows size L can
affect the behavior of the scrolls and also their corresponding MLE. This
make the FOCS even more tunable (Tolba et al., 2017).

14.9 CONCLUSION

This chapter has made a quick overview of the applications of FOCS in vari-
ous scientific and engineering fields. The study of chaos continues to be an
exciting part of studying nonlinear dynamical system. It can be seen that in
some applications chaotic behavior is an advantage while in others it has to
be avoided. The addition of fractional derivatives in the description of cha-
otic systems has increased its complexity and flexibility. This is due to the