Page 63 - Mathematical Techniques of Fractional Order Systems

Nonlinear Fractional Order Boundary-Value Problems Chapter | 2 53

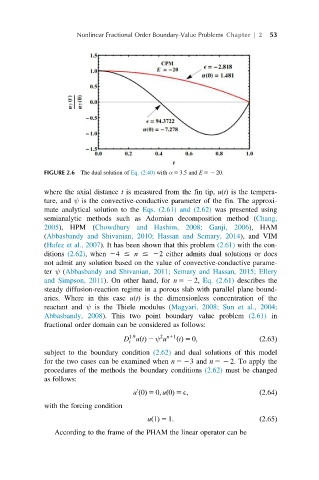
FIGURE 2.6 The dual solution of Eq. (2.40) with α 5 3.5 and E 52 20.

where the axial distance t is measured from the fin tip, u(t) is the tempera-
ture, and ψ is the convective-conductive parameter of the fin. The approxi-
mate analytical solution to the Eqs. (2.61) and (2.62) was presented using
semianalytic methods such as Adomian decomposition method (Chang,
2005), HPM (Chowdhury and Hashim, 2008; Ganji, 2006), HAM
(Abbasbandy and Shivanian, 2010; Hassan and Semary, 2014), and VIM
(Hafez et al., 2007). It has been shown that this problem (2.61) with the con-
ditions (2.62), when 24 # n #22 either admits dual solutions or does
not admit any solution based on the value of convective-conductive parame-
ter ψ (Abbasbandy and Shivanian, 2011; Semary and Hassan, 2015; Ellery
and Simpson, 2011). On other hand, for n 52 2, Eq. (2.61) describes the
steady diffusion-reaction regime in a porous slab with parallel plane bound-
aries. Where in this case u(t) is the dimensionless concentration of the
reactant and ψ is the Thiele modulus (Magyari, 2008; Sun et al., 2004;
Abbasbandy, 2008). This two point boundary value problem (2.61) in
fractional order domain can be considered as follows:
1:9
2 n11
D uðtÞ 2 ψ u ðtÞ 5 0; ð2:63Þ
t
subject to the boundary condition (2.62) and dual solutions of this model
for the two cases can be examined when n 523 and n 52 2. To apply the
procedures of the methods the boundary conditions (2.62) must be changed
as follows:
u ð0Þ 5 0; uð0Þ 5 E; ð2:64Þ
0
with the forcing condition
uð1Þ 5 1: ð2:65Þ
According to the frame of the PHAM the linear operator can be