Page 165 - Mechanical design of microresonators _ modeling and applications

0-07-145538-8_CH03_164_08/30/05

Microhinges and Microcantilevers: Lumped-Parameter Modeling and Design

164 Chapter Three

2.5

2
length [mm] 1.5

1

0.5

0
0 5000 10000 15000 20000
frequency [Hz]
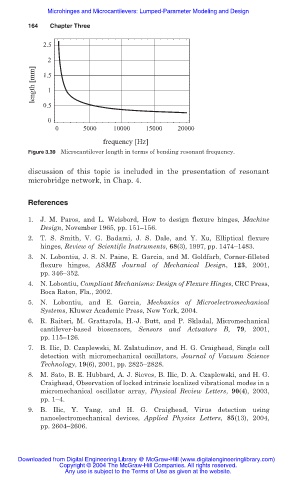
Figure 3.39 Microcantilever length in terms of bending resonant frequency.

discussion of this topic is included in the presentation of resonant
microbridge network, in Chap. 4.

References

1. J. M. Paros, and L. Weisbord, How to design flexure hinges, Machine
Design, November 1965, pp. 151–156.
2. T. S. Smith, V. G. Badami, J. S. Dale, and Y. Xu, Elliptical flexure
hinges, Review of Scientific Instruments, 68(3), 1997, pp. 1474–1483.
3. N. Lobontiu, J. S. N. Paine, E. Garcia, and M. Goldfarb, Corner-filleted
flexure hinges, ASME Journal of Mechanical Design, 123, 2001,
pp. 346–352.
4. N. Lobontiu, Compliant Mechanisms: Design of Flexure Hinges, CRC Press,
Boca Raton, Fla., 2002.
5. N. Lobontiu, and E. Garcia, Mechanics of Microelectromechanical
Systems, Kluwer Academic Press, New York, 2004.
6. R. Raiteri, M. Grattarola, H.-J. Butt, and P. Skladal, Micromechanical
cantilever-based biosensors, Sensors and Actuators B, 79, 2001,
pp. 115–126.
7. B. Ilic, D. Czaplewski, M. Zalatudinov, and H. G. Craighead, Single cell
detection with micromechanical oscillators, Journal of Vacuum Science
Technology, 19(6), 2001, pp. 2825–2828.
8. M. Sato, B. E. Hubbard, A. J. Sieves, B. Ilic, D. A. Czaplewski, and H. G.
Craighead, Observation of locked intrinsic localized vibrational modes in a
micromechanical oscillator array, Physical Review Letters, 90(4), 2003,
pp. 1–4.
9. B. Ilic, Y. Yang, and H. G. Craighead, Virus detection using
nanoelectromechanical devices, Applied Physics Letters, 85(13), 2004,
pp. 2604–2606.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.