Page 83 - Mechanical design of microresonators _ modeling and applications

0-07-145538-8_CH02_82_08/30/05

Basic Members: Lumped- and Distributed-Parameter Modeling and Design

82 Chapter Two

1.04
rm b 1.25

1.01
0.00001
α

t 1 [m] 1.05
0.00005
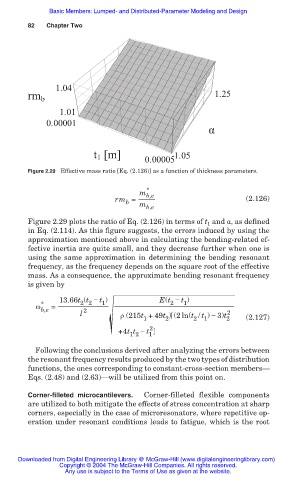
Figure 2.29 Effective mass ratio [Eq. (2.126)] as a function of thickness parameters.

m * b,e
rm = (2.126)
b m b,e
Figure 2.29 plots the ratio of Eq. (2.126) in terms of t 1 and Į, as defined
in Eq. (2.114). As this figure suggests, the errors induced by using the
approximation mentioned above in calculating the bending-related ef-
fective inertia are quite small, and they decrease further when one is
using the same approximation in determining the bending resonant
frequency, as the frequency depends on the square root of the effective
mass. As a consequence, the approximate bending resonant frequency
is given by
13.66t (t í t ) E(t í t )
1
2
2 2
1
Ȧ * b,e = 2
l ȡ (215t +49t ) (2ln(t / t ) í 3)t 2 2 (2.127)
1
1
2
2
+4t t í t 1 2
1 2
Following the conclusions derived after analyzing the errors between
the resonant frequency results produced by the two types of distribution
functions, the ones corresponding to constant-cross-section members–
Eqs. (2.48) and (2.63)–will be utilized from this point on.
Corner-filleted microcantilevers. Corner-filleted flexible components
are utilized to both mitigate the effects of stress concentration at sharp
corners, especially in the case of microresonators, where repetitive op-
eration under resonant conditions leads to fatigue, which is the root

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.