Page 44 - Mechanical Engineer's Data Handbook

STRENGTHS OF MATERIALS 33

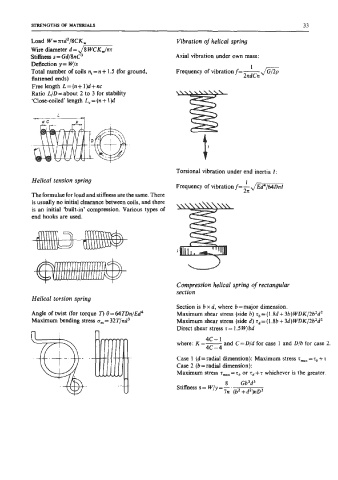
Load W=xzd2/8CK, Vibration of helical spring
Wire diameter d = dmi
Stiffness S= Gd/8nC3 Axial vibration under own mass:
Deflection y= Wls 1
Total number of coils n,=n+ 1.5 (for ground, Frequency of vibration f = -
flattened ends) 2xdCn
Free length L=(n+l)d+nc
Ratio LID = about 2 to 3 for stability
‘Close-coiled‘ length L, = (n + 1 )d

Torsional vibration under end inertia I:
Helical tension spring 1
Frequency of vibration f = z;; d m
The formulae for load and stiffness are the same. There
is usually no initial clearance between coils, and there
is an initial ‘built-in’ compression. Various types of
end hooks are used.

Compression helical spring of rectangular
section
Helical torsion spring
Section is b x d, where b = major dimension.
Angle of twist (for torque r) 8 = 64TDn/Ed4 Maximum shear stress (side b) T*= (1.86 + 36) WDK/2b2dZ
Maximum bending stress 6, = 32T/nd3 Maximum shear stress (side d) T,, = (1.8b + 3d)WDK/2b2d2
Direct shear stress T = 1.5 W/bd
4C-1
where: K =- and C= D/d for case 1 and Dfb for case 2.
4c-4
Case 1 (d = radial dimension): Maximum stress = T~ + T
Case 2 (b = radial dimension):
Maximum stress T,,,,,=T~ or r,+r whichever is the greater.
8 Gb3d3
Stiffness s= W/y=--
7n (b2 +d2)nD3