Page 92 - Mechanical Engineer's Data Handbook

APPLIED MECHANICS 81

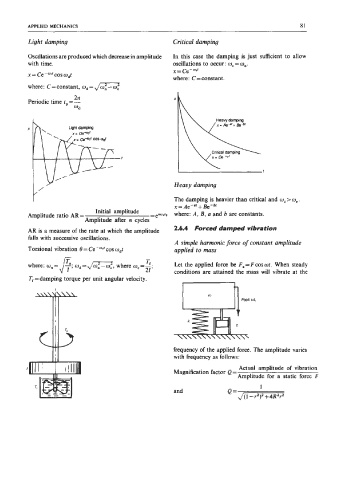
Light damping Critical damping

Oscillations are produced which decrease in amplitude In this case the damping is just sufficient to allow
with time. oscillations to occur: w, = on.
x = ce -wet
x= Ce-wc'coswdt
where: C=constant.
where: C=constant, cod=,/'=
2n
Periodic time t, = -
wd

Heavy damping
/
/
The damping is heavier than critical and w, > 0,.
x = Ae - + Be - bz
Initial amplitude
Amplitude ratio AR = = enw.f, where: A, B, a and b are constants.
Amplitude after n cycles
AR is a measure of the rate at which the amplitude 2.6.4 Forced damped vibration
falls with successive oscillations.
A simple harmonic force of constant amplitude
Torsional vibration 8= Ce-wcfcos mdr applied to mass
JT
where: w, = 3; =JG:, where w, =-, Tf . Let the applied force be Fa = F cos wt. When steady
ad
21
T, =damping torque per unit angular velocity. conditions are attained the mass will vibrate at the

Fcos 01,

frequency of the applied force. The amplitude varies
with frequency as follows:
Actual amplitude of vibration
Magnification factor Q =
Amplitude for a static force F
1
and Q=
J(1 -r2)2+4R2r2