Page 370 - Mechanical Engineers' Handbook (Volume 2)

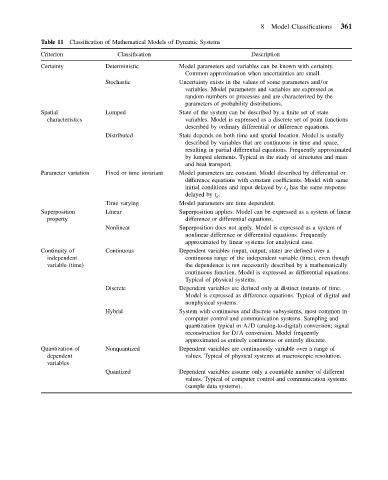
8 Model Classifications 361

Table 11 Classification of Mathematical Models of Dynamic Systems
Criterion Classification Description
Certainty Deterministic Model parameters and variables can be known with certainty.
Common approximation when uncertainties are small.
Stochastic Uncertainty exists in the values of some parameters and/or
variables. Model parameters and variables are expressed as
random numbers or processes and are characterized by the
parameters of probability distributions.
Spatial Lumped State of the system can be described by a finite set of state
characteristics variables. Model is expressed as a discrete set of point functions
described by ordinary differential or difference equations.
Distributed State depends on both time and spatial location. Model is usually
described by variables that are continuous in time and space,
resulting in partial differential equations. Frequently approximated
by lumped elements. Typical in the study of structures and mass
and heat transport.
Parameter variation Fixed or time invariant Model parameters are constant. Model described by differential or
difference equations with constant coefficients. Model with same
initial conditions and input delayed by t d has the same response
delayed by t d .
Time varying Model parameters are time dependent.
Superposition Linear Superposition applies. Model can be expressed as a system of linear
property difference or differential equations.
Nonlinear Superposition does not apply. Model is expressed as a system of
nonlinear difference or differential equations. Frequently
approximated by linear systems for analytical ease.
Continuity of Continuous Dependent variables (input, output, state) are defined over a
independent continuous range of the independent variable (time), even though
variable (time) the dependence is not necessarily described by a mathematically
continuous function. Model is expressed as differential equations.
Typical of physical systems.
Discrete Dependent variables are defined only at distinct instants of time.
Model is expressed as difference equations. Typical of digital and
nonphysical systems.
Hybrid System with continuous and discrete subsystems, most common in
computer control and communication systems. Sampling and
quantization typical in A/D (analog-to-digital) conversion; signal
reconstruction for D/A conversion. Model frequently
approximated as entirely continuous or entirely discrete.
Quantization of Nonquantized Dependent variables are continuously variable over a range of
dependent values. Typical of physical systems at macroscopic resolution.
variables
Quantized Dependent variables assume only a countable number of different
values. Typical of computer control and communication systems
(sample data systems).