Page 98 - Mechanical Engineers' Handbook (Volume 4)

13 Flow Measurements 87

profile drag, depends on the body shape, the Reynolds number, and, usually, the location of
boundary layer transition.
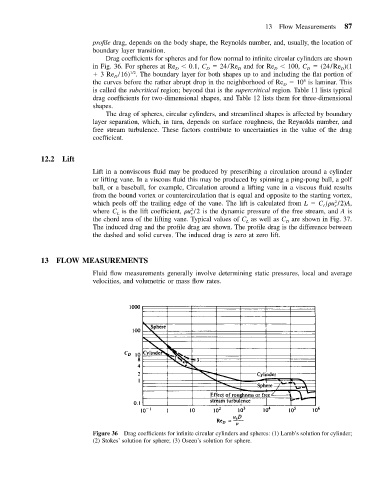
Drag coefficients for spheres and for flow normal to infinite circular cylinders are shown
in Fig. 36. For spheres at Re 0.1, C 24/Re and for Re 100, C (24/Re )(1
D
D
D
D
D
D
3Re /16) . The boundary layer for both shapes up to and including the flat portion of
1/2
D
the curves before the rather abrupt drop in the neighborhood of Re 10 is laminar. This
5
D
is called the subcritical region; beyond that is the supercritical region. Table 11 lists typical
drag coefficients for two-dimensional shapes, and Table 12 lists them for three-dimensional
shapes.
The drag of spheres, circular cylinders, and streamlined shapes is affected by boundary
layer separation, which, in turn, depends on surface roughness, the Reynolds number, and
free stream turbulence. These factors contribute to uncertainties in the value of the drag
coefficient.
12.2 Lift
Lift in a nonviscous fluid may be produced by prescribing a circulation around a cylinder
or lifting vane. In a viscous fluid this may be produced by spinning a ping-pong ball, a golf
ball, or a baseball, for example, Circulation around a lifting vane in a viscous fluid results
from the bound vortex or countercirculation that is equal and opposite to the starting vortex,
which peels off the trailing edge of the vane. The lift is calculated from L C ( u /2)A,
2
L
s
where C is the lift coefficient, u /2 is the dynamic pressure of the free stream, and A is
2
s
L
the chord area of the lifting vane. Typical values of C as well as C are shown in Fig. 37.
D
L
The induced drag and the profile drag are shown. The profile drag is the difference between
the dashed and solid curves. The induced drag is zero at zero lift.
13 FLOW MEASUREMENTS
Fluid flow measurements generally involve determining static pressures, local and average
velocities, and volumetric or mass flow rates.

Figure 36 Drag coefficients for infinite circular cylinders and spheres: (1) Lamb’s solution for cylinder;
(2) Stokes’ solution for sphere; (3) Oseen’s solution for sphere.