Page 380 - Mechanics of Asphalt Microstructure and Micromechanics

372 Ch a p t e r E l ev e n

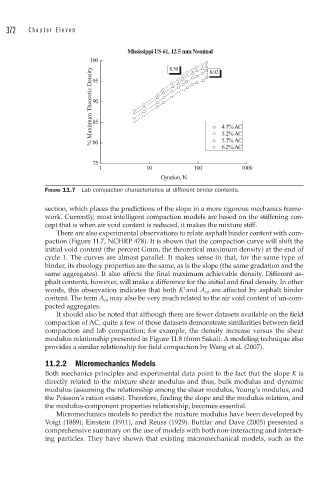
Mississippi US 61, 12.5 mm Nominal
100 8.30 8.02
% Maximum Theoretic Density 90
95

85
4.7% AC
5.2% AC
5.7% AC
80
6.2% AC
75
1 10 100 1000
Gyration, N
FIGURE 11.7 Lab compaction characteristics at different binder contents.

section, which places the predictions of the slope in a more rigorous mechanics frame-
work. Currently, most intelligent compaction models are based on the stiffening con-
cept that is when air void content is reduced, it makes the mixture stiff.
There are also experimental observations to relate asphalt binder content with com-
paction (Figure 11.7, NCHRP 478). It is shown that the compaction curve will shift the
initial void content (the percent Gmm, the theoretical maximum density) at the end of
cycle 1. The curves are almost parallel. It makes sense in that, for the same type of
binder, its rheology properties are the same, as is the slope (the same gradation and the
same aggregates). It also affects the final maximum achievable density. Different as-
phalt contents, however, will make a difference for the initial and final density. In other
words, this observation indicates that both K and A v0 are affected by asphalt binder
l
content. The term A v0 may also be very much related to the air void content of un-com-
pacted aggregates.
It should also be noted that although there are fewer datasets available on the field
compaction of AC, quite a few of those datasets demonstrate similarities between field
compaction and lab compaction; for example, the density increase versus the shear
modulus relationship presented in Figure 11.8 (from Sakai). A modeling technique also
provides a similar relationship for field compaction by Wang et al. (2007).

11.2.2 Micromechanics Models
Both mechanics principles and experimental data point to the fact that the slope K is
directly related to the mixture shear modulus and thus, bulk modulus and dynamic
modulus (assuming the relationship among the shear modulus, Young’s modulus, and
the Poisson’s ration exists). Therefore, finding the slope and the modulus relation, and
the modulus-component properties relationship, becomes essential.
Micromechanics models to predict the mixture modulus have been developed by
Voigt (1889), Einstein (1911), and Reuss (1929). Buttlar and Dave (2005) presented a
comprehensive summary on the use of models with both non-interacting and interact-
ing particles. They have shown that existing micromechanical models, such as the