Page 384 - Mechanics of Asphalt Microstructure and Micromechanics

376 Ch a p t e r E l ev e n

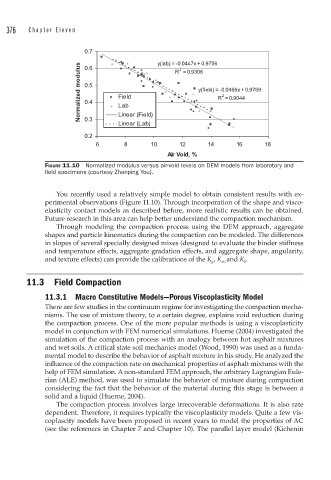
0.7 y(lab) = -0.0447x + 0.9706
Normalized modulus 0.5 Field y(field) = -0.0466x + 0.9769
0.6
2
R = 0.9306

2
R = 0.9044
0.4
Lab
Linear (Field)
0.3
Linear (Lab)
0.2
6 8 10 12 14 16 18
Air Void, %
FIGURE 11.10 Normalized modulus versus air-void levels on DEM models from laboratory and
fi eld specimens (courtesy Zhanping You).

You recently used a relatively simple model to obtain consistent results with ex-
perimental observations (Figure 11.10). Through incorporation of the shape and visco-
elasticity contact models as described before, more realistic results can be obtained.
Future research in this area can help better understand the compaction mechanism.
Through modeling the compaction process using the DEM approach, aggregate
shapes and particle kinematics during the compaction can be modeled. The differences
in slopes of several specially designed mixes (designed to evaluate the binder stiffness
and temperature effects, aggregate gradation effects, and aggregate shape, angularity,
and texture effects) can provide the calibrations of the K g , K m, and K b .

11.3 Field Compaction

11.3.1 Macro Constitutive Models—Porous Viscoplasticity Model
There are few studies in the continuum regime for investigating the compaction mecha-
nisms. The use of mixture theory, to a certain degree, explains void reduction during
the compaction process. One of the more popular methods is using a viscoplasticity
model in conjunction with FEM numerical simulations. Huerne (2004) investigated the
simulation of the compaction process with an analogy between hot asphalt mixtures
and wet soils. A critical state soil mechanics model (Wood, 1990) was used as a funda-
mental model to describe the behavior of asphalt mixture in his study. He analyzed the
influence of the compaction rate on mechanical properties of asphalt mixtures with the
help of FEM simulation. A non-standard FEM approach, the arbitrary Lagrangian Eule-
rian (ALE) method, was used to simulate the behavior of mixture during compaction
considering the fact that the behavior of the material during this stage is between a
solid and a liquid (Huerne, 2004).
The compaction process involves large irrecoverable deformations. It is also rate
dependent. Therefore, it requires typically the viscoplasticity models. Quite a few vis-
coplascity models have been proposed in recent years to model the properties of AC
(see the references in Chapter 7 and Chapter 10). The parallel layer model (Kichenin