Page 381 - Mechanics of Asphalt Microstructure and Micromechanics

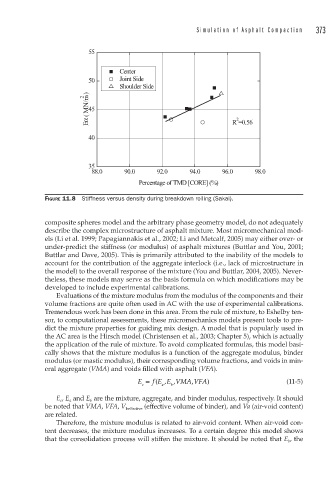
Simulation of Asphalt Compaction 373

55

Center
50 Joint Side
Shoulder Side
Eα (MN/m) 45 R =0.56
2

2

40

35
88.0 90.0 92.0 94.0 96.0 98.0
Percentage of TMD [CORE] (%)
FIGURE 11.8 Stiffness versus density during breakdown rolling (Sakai).

composite spheres model and the arbitrary phase geometry model, do not adequately
describe the complex microstructure of asphalt mixture. Most micromechanical mod-
els (Li et al. 1999; Papagiannakis et al., 2002; Li and Metcalf, 2005) may either over- or
under-predict the stiffness (or modulus) of asphalt mixtures (Buttlar and You, 2001;
Buttlar and Dave, 2005). This is primarily attributed to the inability of the models to
account for the contribution of the aggregate interlock (i.e., lack of microstructure in
the model) to the overall response of the mixture (You and Buttlar, 2004, 2005). Never-
theless, these models may serve as the basis formula on which modifications may be
developed to include experimental calibrations.
Evaluations of the mixture modulus from the modulus of the components and their
volume fractions are quite often used in AC with the use of experimental calibrations.
Tremendous work has been done in this area. From the rule of mixture, to Eshelby ten-
sor, to computational assessments, these micromechanics models present tools to pre-
dict the mixture properties for guiding mix design. A model that is popularly used in
the AC area is the Hirsch model (Christensen et al., 2003; Chapter 5), which is actually
the application of the rule of mixture. To avoid complicated formulas, this model basi-
cally shows that the mixture modulus is a function of the aggregate modulus, binder
modulus (or mastic modulus), their corresponding volume fractions, and voids in min-
eral aggregate (VMA) and voids filled with asphalt (VFA).
f E E VMA VFA)
E = (, , , (11-5)
c a b
E c , E a and E b are the mixture, aggregate, and binder modulus, respectively. It should
be noted that VMA, VFA, V beffective (effective volume of binder), and Va (air-void content)
are related.
Therefore, the mixture modulus is related to air-void content. When air-void con-
tent decreases, the mixture modulus increases. To a certain degree this model shows
that the consolidation process will stiffen the mixture. It should be noted that E b , the