Page 117 - Mechanism and Theory in Organic Chemistry

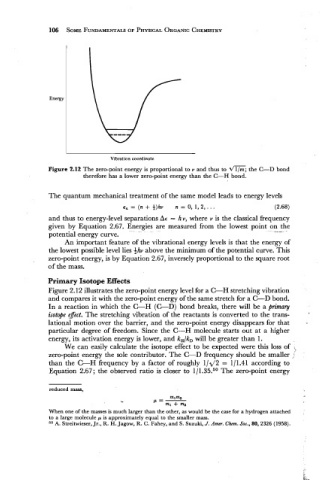
Vibration coordinate
Figure 2.12 The zero-point energy is proportional to v and thus to dm the C-D bond
therefore has a lower zero-point energy than the C-H bond.

The quantum mechanical treatment of the same model leads to energy levels

and thus to energy-level separations Ae = hv, where v is the classical frequency
given by Equation 2.67. Energies are measured from the lowest point on the
potential energy curve.
An important feature of the vibrational energy levels is that the energy of
the lowest possible level lies 3hv above the minimum of the potential curve. This
zero-point energy, is by Equation 2.67, inversely proportional to the square root
of the mass.

Primary Isotope Effects
Figure 2.12 illustrates the zero-point energy level for a C-H stretching vibration
and compares it with the zero-point energy of the same stretch for a C-D bond.
In a reaction in which the GH (GD) bond breaks, there will be a primary
isotope effect. The stretching vibration of the reactants is converted to the trans-
lational motion over the barrier, and the zero-point energy disappears for that -
particular degree of freedom. Since the C-H molecule starts out at a higher
energy, its activation energy is lower, and k,/k, will be greater than 1.
We can easily calculate the isotope effect to be expected were this loss of
zero-point energy the sole contributor. The C-D frequency should be smaller :
than the GH frequency by a factor of roughly 1/d2 = 111.41 according to
Equation 2.67 ; the observed ratio is closer to 1/1.35.50 The zero-point energy

reduced mass,

When one of the masses is much larger than the other, as would be the case for a hydrogen attached
to a large molecule p is approximately equal to the smaller mass.
60 A. Streitwieser, Jr., R. H. Jagow, R. C. Fahey, and S. Suzuki, J. Amer. Chem. Soc., 80, 2326 (1958).