Page 55 - Mechanism and Theory in Organic Chemistry

The hybrids therefore have the form of Equations A1.3.

We assume that s, p,, p,, p, are all normalized and mutually orthogonal.
The requirement that the xi will also be normalized and mutually orthogonal
then leads to the following conditions :
Normalization of xi: ail2 + ala2 + + ata2 = 1 (A1.4)

(The reader familiar with vectors will recognize that, if the xi are thought of as
vectors written in terms of the set of unit vectors s, p,, p,, p,, Equation A1.4 is
just the requirement that xi be of unit length, and Equation A1.5 is the require-
ment that the dot product xi. xj be zero.)
Since the sums of squares of the a coefficients of a given hybrid is unity
(equation A1.4), it is reasonable to take the squares of thexoefficients as giving
the contributions of the orbitals of the s, p,, p,, p, set to the hybrids. We therefore
define the fractional s character of hybrid xi as ail2 and the fractional p character
as aiZ2 + + The orthogonality and normalization conditions guarantee
that the sum of squares of a coefficients down a column in A1.3 will be unity, just
as it is along a row; the fractional contribution of a given member of the s, p,, p,,
p, set summed over all the hybrids (for example all2 + + aSl2 + for
the s-orbital contributions) therefore will always be unity.
Equations A1.3 can be put in a more convenient form in the following way.
We note that because the s orbital is spherically symmetrical, the directional

7 I sin e sin 6

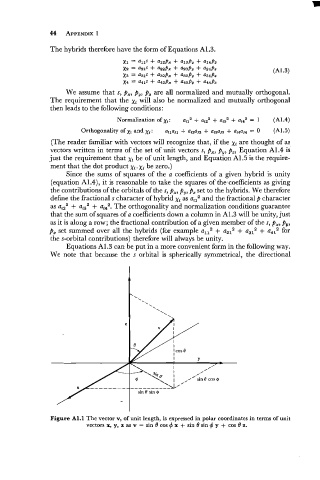
Figure Al.l The vector v, of unit length, is expressed in polar coordinates in terms of unit
vectors x, y, z as v = sin 0 cos 4 x + sin 0 sin 4 y + cos 0 z.