Page 396 - Microsensors, MEMS and Smart Devices - Gardner Varadhan and Awadelkarim

376 IDT MICROSENSORS

0.00 0.20 0.40 0.60 0.80 1.00
Normalized distance

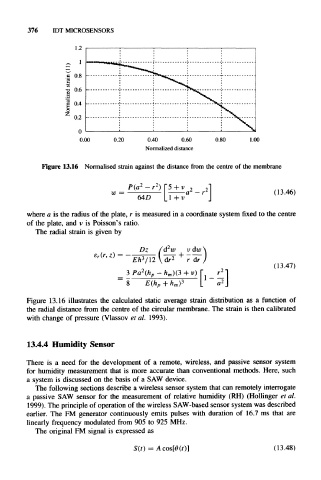
Figure 13.16 Normalised strain against the distance from the centre of the membrane

2
P(a 2 – r )
w = (13.46)
64D
where a is the radius of the plate, r is measured in a coordinate system fixed to the centre
of the plate, and v is Poisson's ratio.
The radial strain is given by
2
r(r,z) = Dz d w + vdw
~~ ~
(13.47)
8 E(h 1

Figure 13.16 illustrates the calculated static average strain distribution as a function of
the radial distance from the centre of the circular membrane. The strain is then calibrated
with change of pressure (Vlassov et al. 1993).

13.4.4 Humidity Sensor

There is a need for the development of a remote, wireless, and passive sensor system
for humidity measurement that is more accurate than conventional methods. Here, such
a system is discussed on the basis of a SAW device.
The following sections describe a wireless sensor system that can remotely interrogate
a passive SAW sensor for the measurement of relative humidity (RH) (Hollinger et al.
1999). The principle of operation of the wireless SAW-based sensor system was described
earlier. The FM generator continuously emits pulses with duration of 16.7 ms that are
linearly frequency modulated from 905 to 925 MHz.
The original FM signal is expressed as

= Acos[0(t)] (13.48)