Page 179 - MODELING OF ASPHALT CONCRETE

Interr elationships among Asphalt Concr ete Stif fnesses 157

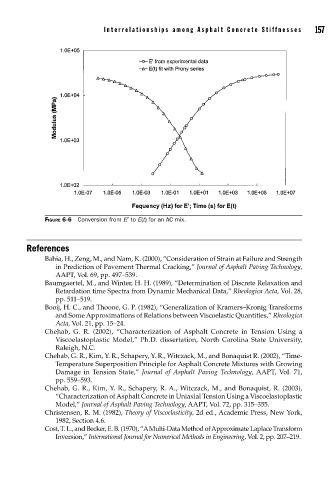
FIGURE 6-6 Conversion from E′ to E(t) for an AC mix.

References
Bahia, H., Zeng, M., and Nam, K. (2000), “Consideration of Strain at Failure and Strength
in Prediction of Pavement Thermal Cracking,” Journal of Asphalt Paving Technology,
AAPT, Vol. 69, pp. 497–539.
Baumgaertel, M., and Winter, H. H. (1989), “Determination of Discrete Relaxation and
Retardation time Spectra from Dynamic Mechanical Data,” Rheologica Acta, Vol. 28,
pp. 511–519.
Booij, H. C., and Thoone, G. P. (1982), “Generalization of Kramers–Kronig Transforms
and Some Approximations of Relations between Viscoelastic Quantities,” Rheologica
Acta, Vol. 21, pp. 15–24.
Chehab, G. R. (2002), “Characterization of Asphalt Concrete in Tension Using a
Viscoelastoplastic Model,” Ph.D. dissertation, North Carolina State University,
Raleigh, N.C.
Chehab, G. R., Kim, Y. R., Schapery, Y. R., Witczack, M., and Bonaquist R. (2002), “Time-
Temperature Superposition Principle for Asphalt Concrete Mixtures with Growing
Damage in Tension State,” Journal of Asphalt Paving Technology, AAPT, Vol. 71,
pp. 559–593.
Chehab, G. R., Kim, Y. R., Schapery, R. A., Witczack, M., and Bonaquist, R. (2003),
“Characterization of Asphalt Concrete in Uniaxial Tension Using a Viscoelastoplastic
Model,” Journal of Asphalt Paving Technology, AAPT, Vol. 72, pp. 315–355.
Christensen, R. M. (1982), Theory of Viscoelasticity, 2d ed., Academic Press, New York,
1982, Section 4.6.
Cost, T. L., and Becker, E. B. (1970), “A Multi-Data Method of Approximate Laplace Transform
Inversion,” International Journal for Numerical Methods in Engineering, Vol. 2, pp. 207–219.