Page 281 - Modern Control Systems

Section 4.8 Design Examples 255
output due to the two inputs is
K + lis 1
Y(s) = 2 R{s) + 2 Us). (4.57)
s + 125 + K s + 12s + K
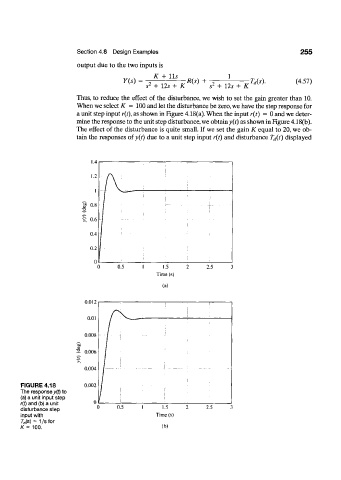
Thus, to reduce the effect of the disturbance, we wish to set the gain greater than 10.
When we select K = 100 and let the disturbance be zero, we have the step response for
a unit step input r(t), as shown in Figure 4.18(a). When the input r(t) = 0 and we deter-
mine the response to the unit step disturbance, we obtain y(t) as shown in Figure 4.18(b).
The effect of the disturbance is quite small. If we set the gain K equal to 20, we ob-
tain the responses of y(t) due to a unit step input r(t) and disturbance T d(t) displayed

(a)

0.012

0.01

0.008 / i * ' ' i
/
0.006

0.004

FIGURE 4.18 0.002
The response y{t) to
(a) a unit input step
r(t) and (b) a unit 0
disturbance step 0 0.5 1 1.5 2 2.5
input with Time (s)
TJs) = 1/sfor
K = 100. (b)