Page 304 - Modern Control Systems

278 Chapter 4 Feedback Control System Characteristics

The loop gain L(s) = G c(s)G(s) plays a fundamental role in control system
analysis. Associated with the loop gain we can define the sensitivity and comple-
mentary sensitivity functions as
1 . - - L(s)
S(s) and C(s) =
1 + L(s) 1 + L(sY
respectively. The tracking error is given by
E(s) = S(s)R(s) - S(s)G(s)T d(s) + C(s)N(s).
In order to minimize the tracking error, E(s), we desire to make S(s) and C(s) small.
Because the sensitivity and complementary sensitivity functions satisfy the con-
straint

S(s) + C(s) = 1,
we are faced with the fundamental trade-off in control system design between
rejecting disturbances and reducing sensitivity to plant changes on the one hand,
and attenuating measurement noise on the other hand.
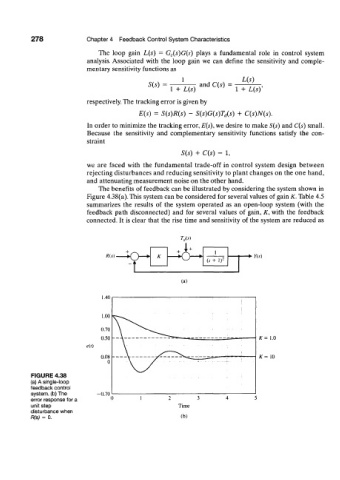
The benefits of feedback can be illustrated by considering the system shown in
Figure 4.38(a). This system can be considered for several values of gain K. Table 4.5
summarizes the results of the system operated as an open-loop system (with the
feedback path disconnected) and for several values of gain, K, with the feedback
connected. It is clear that the rise time and sensitivity of the system are reduced as

R(s) ** Y(s)

(a)

1.40

K= 1.0
e(t)
K= 10

FIGURE 4.38
(a) A single-loop
feedback control
system, (b) The
error response for a
unit step
disturbance when
R(s) = 0.