Page 303 - Modern Control Systems

Section 4.11 Summary 277

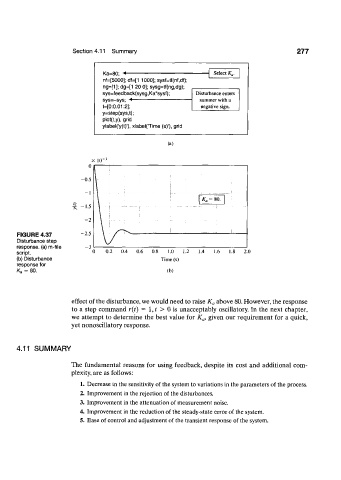
Ka=80; < Select K„.
nf=[5000]; df=[1 1000]; sysf=tf(nf,df);
ng=[1]; dg=[1 20 0]; sysg=tf(ng,dg);
sys=feedback(sysg,Ka*sysf); Disturbance enters
sys=-sys; ** summer with a
t=[0:0.01:2J; negative sign.
y=step(sys,t);
plot(t.y), grid
ylabel('y(t)'), xIabel(Time (s)'), grid

(a)

x 10"
0

-0.5
- 1 \ , • • I ;
In ;
\ : '• K a = 80.
S -1.5
- 2

FIGURE 4.37 -2.5 i
Disturbance step I/
response, (a) m-file -3
script. 0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.8 2.0
(b) Disturbance Time (s)
response for
= 80. (b)
K a

effect of the disturbance, we would need to raise K a above 80. However, the response
to a step command r{t) = 1, t > 0 is unacceptably oscillatory. In the next chapter,
we attempt to determine the best value for K a, given our requirement for a quick,
yet nonoscillatory response.

4.11 SUMMARY

The fundamental reasons for using feedback, despite its cost and additional com-
plexity, are as follows:

1. Decrease in the sensitivity of the system to variations in the parameters of the process.
2. Improvement in the rejection of the disturbances.
3. Improvement in the attenuation of measurement noise.
4. Improvement in the reduction of the steady-state error of the system.
5. Ease of control and adjustment of the transient response of the system.