Page 330 - MODERN ELECTROCHEMISTRY

266 CHAPTER 3

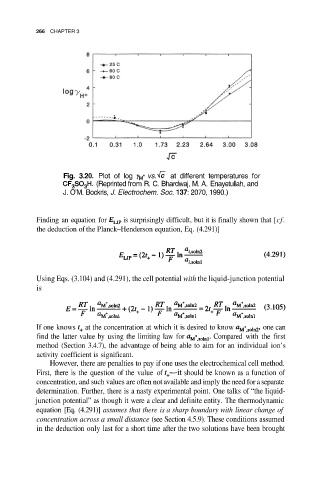
Fig. 3.20. Plot of log vs. at different temperatures for
(Reprinted from R. C. Bhardwaj, M. A. Enayetullah, and
J. O’M. Bockris, J. Electrochem. Soc. 137: 2070, 1990.)

Finding an equation for is surprisingly difficult, but it is finally shown that [cf.
the deduction of the Planck–Henderson equation, Eq. (4.291)]

Using Eqs. (3.104) and (4.291), the cell potential with the liquid-junction potential
is

If one knows at the concentration at which it is desired to know one can
find the latter value by using the limiting law for Compared with the first
method (Section 3.4.7), the advantage of being able to aim for an individual ion’s
activity coefficient is significant.
However, there are penalties to pay if one uses the electrochemical cell method.
First, there is the question of the value of should be known as a function of
concentration, and such values are often not available and imply the need for a separate
determination. Further, there is a nasty experimental point. One talks of “the liquid-
junction potential” as though it were a clear and definite entity. The thermodynamic
equation [Eq. (4.291)] assumes that there is a sharp boundary with linear change of
concentration across a small distance (see Section 4.5.9). These conditions assumed
in the deduction only last for a short time after the two solutions have been brought