Page 338 - MODERN ELECTROCHEMISTRY

274 CHAPTER 3

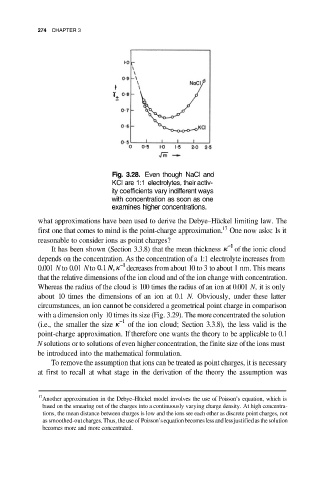
Fig. 3.28. Even though NaCl and
KCl are 1:1 electrolytes, their activ-
ity coefficients vary indifferent ways
with concentration as soon as one
examines higher concentrations.

what approximations have been used to derive the Debye–Hückel limiting law. The
17
first one that comes to mind is the point-charge approximation. One now asks: Is it
reasonable to consider ions as point charges?
It has been shown (Section 3.3.8) that the mean thickness of the ionic cloud
depends on the concentration. As the concentration of a 1:1 electrolyte increases from
0.001 N to 0.01 Nto decreases from about 10 to 3 to about 1 nm. This means
that the relative dimensions of the ion cloud and of the ion change with concentration.
Whereas the radius of the cloud is 100 times the radius of an ion at 0.001 N, it is only
about 10 times the dimensions of an ion at 0.1 N. Obviously, under these latter
circumstances, an ion cannot be considered a geometrical point charge in comparison
with a dimension only 10 times its size (Fig. 3.29). The more concentrated the solution
(i.e., the smaller the size of the ion cloud; Section 3.3.8), the less valid is the
point-charge approximation. If therefore one wants the theory to be applicable to 0.1
N solutions or to solutions of even higher concentration, the finite size of the ions must
be introduced into the mathematical formulation.
To remove the assumption that ions can be treated as point charges, it is necessary
at first to recall at what stage in the derivation of the theory the assumption was

17
Another approximation in the Debye–Hückel model involves the use of Poisson’s equation, which is
based on the smearing out of the charges into a continuously varying charge density. At high concentra-
tions, the mean distance between charges is low and the ions see each other as discrete point charges, not
as smoothed-out charges. Thus, the use of Poisson’s equation becomes less and less justified as the solution
becomes more and more concentrated.