Page 24 - Modern Optical Engineering The Design of Optical Systems

Optics Overview 7

Since Snell’s law relates the sines of the angles between a light ray and
the normal to the surface, it is readily applicable to surfaces other than
the plane which we used in the example above; the path of a light ray may
be calculated through any surface for which we can determine the point
of intersection of the ray and the normal to the surface at that point.
The angle I 1 between the incident ray and surface normal is custo-
marily referred to as the angle of incidence; the angle I 2 is called the
angle of refraction.
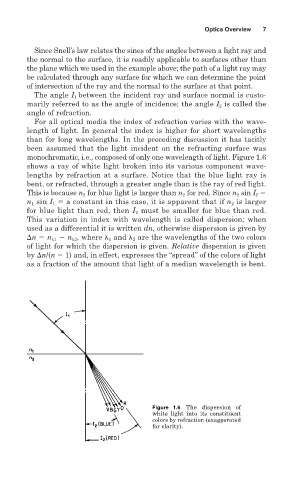
For all optical media the index of refraction varies with the wave-
length of light. In general the index is higher for short wavelengths
than for long wavelengths. In the preceding discussion it has tacitly
been assumed that the light incident on the refracting surface was
monochromatic, i.e., composed of only one wavelength of light. Figure 1.6
shows a ray of white light broken into its various component wave-
lengths by refraction at a surface. Notice that the blue light ray is
bent, or refracted, through a greater angle than is the ray of red light.
This is because n 2 for blue light is larger than n 2 for red. Since n 2 sin I 2
n 1 sin I 1 a constant in this case, it is apparent that if n 2 is larger
for blue light than red, then I 2 must be smaller for blue than red.
This variation in index with wavelength is called dispersion; when
used as a differential it is written dn, otherwise dispersion is given by

n n 1 n 2 , where 1 and 2 are the wavelengths of the two colors
of light for which the dispersion is given. Relative dispersion is given
by
n/(n 1) and, in effect, expresses the “spread” of the colors of light
as a fraction of the amount that light of a median wavelength is bent.

Figure 1.6 The dispersion of
white light into its constituent
colors by refraction (exaggerated
for clarity).