Page 126 - Neural Network Modeling and Identification of Dynamical Systems

3.4 ANN-BASED CONTROL OF DYNAMICAL SYSTEMS 115

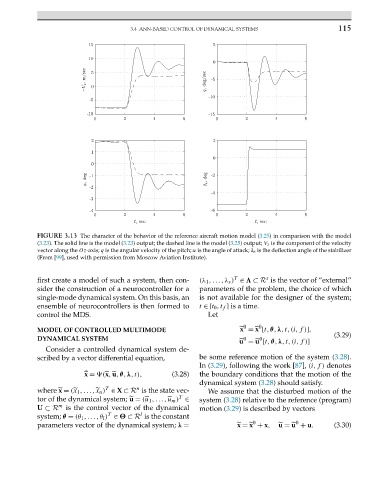
FIGURE 3.13 The character of the behavior of the reference aircraft motion model (3.25) incomparisonwiththe model
(3.23). The solid line is the model (3.23) output; the dashed line is the model (3.25)output; V z is the component of the velocity
vector along the Oz-axis; q is the angular velocity of the pitch; α is the angle of attack; δ e is the deflection angle of the stabilizer
(From [99], used with permission from Moscow Aviation Institute).

s
T
first create a model of such a system, then con- (λ 1 ,...,λ s ) ∈ ⊂ R is the vector of “external”
sider the construction of a neurocontroller for a parameters of the problem, the choice of which
single-mode dynamical system. On this basis, an is not available for the designer of the system;
ensemble of neurocontrollers is then formed to t ∈[t 0 ,t f ] is a time.
control the MDS. Let
0
0
MODEL OF CONTROLLED MULTIMODE x = x [t,θ,λ,t,(i,f )],
(3.29)
DYNAMICAL SYSTEM 0 0
u = u [t,θ,λ,t,(i,f )]
Consider a controlled dynamical system de-
scribed by a vector differential equation, be some reference motion of the system (3.28).
In (3.29), following the work [87], (i,f ) denotes
˙ x = ( x, u,θ,λ,t), (3.28) the boundary conditions that the motion of the
dynamical system (3.28) should satisfy.
n
T
where x = ( 1 ,..., x n ) ∈ X ⊂ R is the state vec- We assume that the disturbed motion of the
x
T
u
tor of the dynamical system; u = ( 1 ,..., u m ) ∈ system (3.28) relative to the reference (program)
m
U ⊂ R is the control vector of the dynamical motion (3.29) is described by vectors
T
l
system; θ = (θ 1 ,...,θ l ) ∈ ⊂ R is the constant
0
0
parameters vector of the dynamical system; λ = x = x + x, u = u + u. (3.30)