Page 125 - Neural Network Modeling and Identification of Dynamical Systems

114 3. NEURAL NETWORK BLACK BOX APPROACH TO THE MODELING AND CONTROL OF DYNAMICAL SYSTEMS

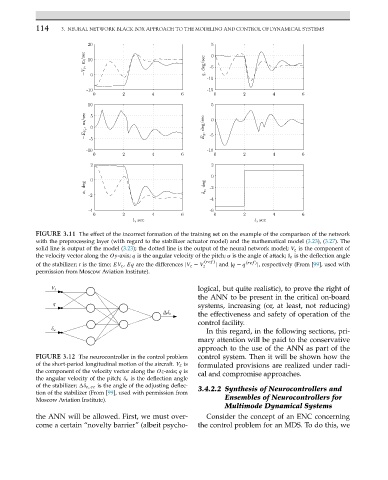
FIGURE 3.11 The effect of the incorrect formation of the training set on the example of the comparison of the network
with the preprocessing layer (with regard to the stabilizer actuator model) and the mathematical model (3.23), (3.27). The
solid line is output of the model (3.23); the dotted line is the output of the neural network model; V z is the component of
the velocity vector along the Oy-axis; q is the angular velocity of the pitch; α is the angle of attack; δ e is the deflection angle
(ref ) (ref )
of the stabilizer; t is the time; EV z , Eq are the differences |V z − V z | and |q − q |, respectively (From [99], used with
permission from Moscow Aviation Institute).
logical, but quite realistic), to prove the right of
the ANN to be present in the critical on-board
systems, increasing (or, at least, not reducing)
the effectiveness and safety of operation of the
control facility.
In this regard, in the following sections, pri-
mary attention will be paid to the conservative
approach to the use of the ANN as part of the
FIGURE 3.12 The neurocontroller in the control problem control system. Then it will be shown how the
of the short-period longitudinal motion of the aircraft. V z is formulated provisions are realized under radi-
the component of the velocity vector along the Oz-axis; q is cal and compromise approaches.
the angular velocity of the pitch; δ e is the deflection angle
of the stabilizer; δ e, cc is the angle of the adjusting deflec- 3.4.2.2 Synthesis of Neurocontrollers and
tion of the stabilizer (From [99], used with permission from
Moscow Aviation Institute). Ensembles of Neurocontrollers for
Multimode Dynamical Systems
the ANN will be allowed. First, we must over- Consider the concept of an ENC concerning
come a certain “novelty barrier” (albeit psycho- the control problem for an MDS. To do this, we