Page 162 - Neural Network Modeling and Identification of Dynamical Systems

152 4. NEURAL NETWORK BLACK BOX MODELING OF AIRCRAFT CONTROLLED MOTION

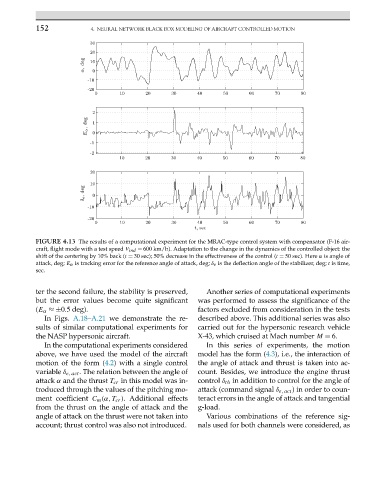
FIGURE 4.13 The results of a computational experiment for the MRAC-type control system with compensator (F-16 air-
craft, flight mode with a test speed V ind = 600 km/h). Adaptation to the change in the dynamics of the controlled object: the
shift of the centering by 10% back (t = 30 sec); 50% decrease in the effectiveness of the control (t = 50 sec). Here α is angle of
attack, deg; E α is tracking error for the reference angle of attack, deg; δ e is the deflection angle of the stabilizer, deg; t is time,
sec.

ter the second failure, the stability is preserved, Another series of computational experiments
but the error values become quite significant was performed to assess the significance of the
(E α ≈±0.5 deg). factors excluded from consideration in the tests
In Figs. A.18–A.21 we demonstrate the re- described above. This additional series was also
sults of similar computational experiments for carried out for the hypersonic research vehicle
the NASP hypersonic aircraft. X-43, which cruised at Mach number M = 6.
In the computational experiments considered In this series of experiments, the motion
above, we have used the model of the aircraft model has the form (4.3), i.e., the interaction of
motion of the form (4.2) with a single control the angle of attack and thrust is taken into ac-
variable δ e, act . The relation between the angle of count. Besides, we introduce the engine thrust
attack α and the thrust T cr in this model was in- control δ th in addition to control for the angle of
troduced through the values of the pitching mo- attack (command signal δ e, act ) in order to coun-
ment coefficient C m (α,T cr ). Additional effects teract errors in the angle of attack and tangential
from the thrust on the angle of attack and the g-load.
angle of attack on the thrust were not taken into Various combinations of the reference sig-
account; thrust control was also not introduced. nals used for both channels were considered, as