Page 226 - Numerical Methods for Chemical Engineering

Gradient methods 215

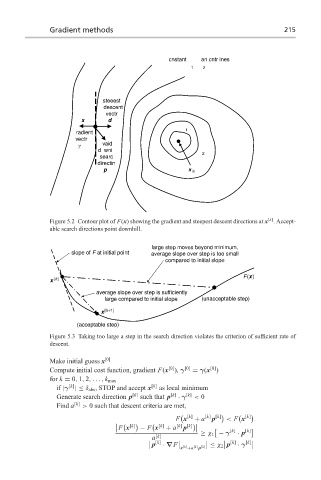
cnstant an cntr ines
1 2

steeest
descent
vectr
x d
1
radient
vectr
γ vaid
d wni
2
searc
directin
p x in

[k]
Figure 5.2 Contour plot of F(x) showing the gradient and steepest descent directions at x . Accept-
able search directions point downhill.

large step moves beyond minimum,
slope of F at initial point average slope over step is too small
compared to initial slope

F(x)
x [k]
average slope over step is sufficiently
large compared to initial slope (unacceptable step)
x [k+1]

(acceptable step)
Figure 5.3 Taking too large a step in the search direction violates the criterion of sufficient rate of
descent.

Make initial guess x [0]
[0]
[0]
Compute initial cost function, gradient F(x ), γ [0] = γ(x )
for k = 0, 1, 2,..., k max
[k]
if |γ |≤ δ abs , STOP and accept x [k] as local minimum
Generate search direction p [k] such that p [k] · γ [k] < 0
Find a [k] > 0 such that descent criteria are met,
[k] [k] [k] [k]
F x + a p < F x

F x
p
[k] − F x [k] + a [k] [k] [k] [k]
≥ χ 1 − γ · p
[k]
[k]
[k] · ∇F [k] ≤ χ 2 p · γ [k]

a

p

[k]
x +a [k] p