Page 227 - Numerical Methods for Chemical Engineering

216 5 Numerical optimization

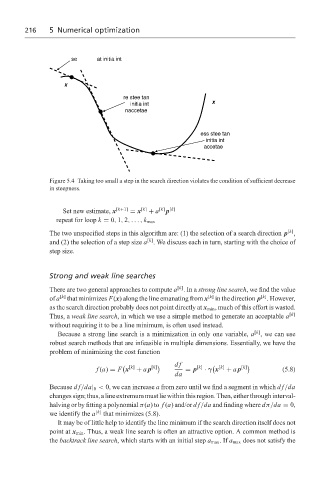
se at initia int

x
re stee tan
initia int x
naccetae

ess stee tan
initia int
accetae

Figure 5.4 Taking too small a step in the search direction violates the condition of sufficient decrease
in steepness.

Set new estimate, x [k+1] = x [k] + a [k] [k]
p
repeat for loop k = 0, 1, 2,..., k max
[k]
The two unspecified steps in this algorithm are: (1) the selection of a search direction p ,
[k]
and (2) the selection of a step size a . We discuss each in turn, starting with the choice of
step size.

Strong and weak line searches
[k]
There are two general approaches to compute a .Ina strong line search, we find the value
[k]
of a [k] that minimizes F(x) along the line emanating from x [k] in the direction p . However,
as the search direction probably does not point directly at x min , much of this effort is wasted.
Thus, a weak line search, in which we use a simple method to generate an acceptable a [k]
without requiring it to be a line minimum, is often used instead.
[k]
Because a strong line search is a minimization in only one variable, a , we can use
robust search methods that are infeasible in multiple dimensions. Essentially, we have the
problem of minimizing the cost function
df
[k] [k] [k] [k] [k]
f (a) = F x + a p = p · γ x + a p (5.8)
da
Because df/da| 0 < 0, we can increase a from zero until we find a segment in which df/da
changes sign; thus, a line extremum must lie within this region. Then, either through interval-
halving or by fitting a polynomial π(a)to f (a) and/or df/da and finding where dπ/da = 0,
we identify the a [k] that minimizes (5.8).
It may be of little help to identify the line minimum if the search direction itself does not
point at x min . Thus, a weak line search is often an attractive option. A common method is
the backtrack line search, which starts with an initial step a max .If a max does not satisfy the