Page 242 - Numerical Methods for Chemical Engineering

Lagrangian methods for constrained optimization 231

Table 5.1 Measured substrate
concentration (in M) in batch
enzymatic reactor

time (min) [S] (M)

30 1.87
60 1.73
90 1.58
120 1.43
180 1.07
240 0.63
300 0.12
315 0.04
330 0.01

2
1
1
1
12
1

2
1 1 2 2
tie in
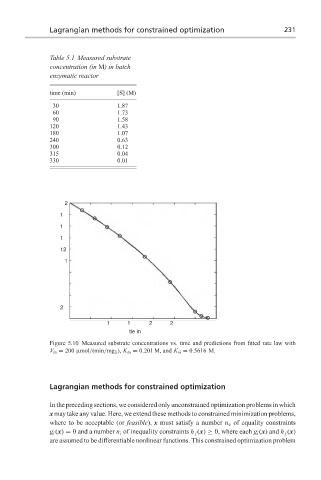
Figure 5.10 Measured substrate concentrations vs. time and predictions from fitted rate law with
V m = 200 µmol/(min/mg E ), K m = 0.201 M, and K si = 0.5616 M.

Lagrangian methods for constrained optimization

In the preceding sections, we considered only unconstrained optimization problems in which
x may take any value. Here, we extend these methods to constrained minimization problems,
where to be acceptable (or feasible), x must satisfy a number n e of equality constraints
g i (x) = 0 and a number n i of inequality constraints h j (x) ≥ 0, where each g i (x) and h j (x)
are assumed to be differentiable nonlinear functions. This constrained optimization problem