Page 147 - Organic Electronics in Sensors and Biotechnology

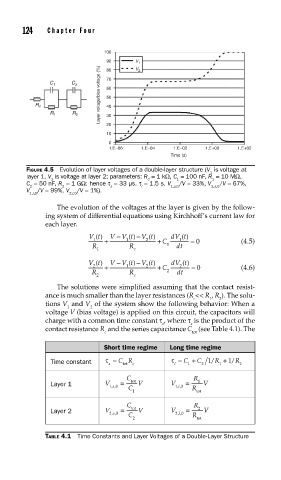
124 Cha pte r F o u r

100
90 V
1 2
Layer voltage/bias voltage (%) 50
V
80
C 70
C 1
2 60
R c 40
R 1 R 2 30
20
10
0
1.E–06 1.E–04 1.E–02 1.E+00 1.E+02
Time (s)

FIGURE 4.5 Evolution of layer voltages of a double-layer structure (V is voltage at
1
layer 1, V is voltage at layer 2; parameters: R = 1 kΩ, C = 100 nF, R = 10 MΩ,
2 C 1 1
C = 50 nF, R = 1 GΩ; hence τ = 33 μs, τ = 1.5 s, V /V = 33%, V /V = 67%,
2 2 s l 1,s,0 2,s,0
V /V = 99%, V /V = 1%).
1,l,0 2,l,0
The evolution of the voltages at the layer is given by the follow-
ing system of differential equations using Kirchhoff’s current law for
each layer.
Vt () VV t ()− − V t () dV t ()
1 + 1 2 + C 1 = 0 (4.5)
R R 1 dt
1 c
Vt () VV t ()− − V t () dV t ()
2 + 1 2 + C 2 = 0 (4.6)
R R 2 dt
2 c
The solutions were simplified assuming that the contact resist-
ance is much smaller than the layer resistances (R << R , R ). The solu-
c 1 2
tions V and V of the system show the following behavior: When a
1 2
voltage V (bias voltage) is applied on this circuit, the capacitors will
charge with a common time constant τ , where τ is the product of the
s s
contact resistance R and the series capacitance C (see Table 4.1). The
c tot
Short time regime Long time regime
Time constant τ = CR c τ = C + C 1/ R + 1/ R 2
l
1
tot
s
1
2
C R
Layer 1 V 1,, s 0 = tot V V 10 = 1 V
l ,,
C
1 R tot
C R
Layer 2 V 2,, s 0 = tot V V 2,, l 0 = 2 V
C
2 R tot
TABLE 4.1 Time Constants and Layer Voltages of a Double-Layer Structure