Page 40 - Organic Electronics in Sensors and Biotechnology

Scaling Effects in Organic Transistors and Transistor-Based Chemical Sensors 17

10 –1 10 –1
10 –2 10 –2
Mobility [cm 2 /(V·s)] 10 –3 5 μm Mobility [cm 2 /(V·s)] 10 –3 5 μm

10 –4
10 –4
2 μm
2 μm
500 nm
500 nm
10 –5 1 μm 10 –5 1 μm
270 nm 270 nm
Envelope fit Envelope fit
10 –6 10 –6
0 200 400 600 800 0 200 400 600 800
290 K sqrt (V ds /L) (V/cm) 1/2 170 K sqrt (V ds /L) (V/cm) 1/2
V g = –40 V V g = –40 V
(a) (b)
10 –1 10 –1
10 –2 10 –2
Mobility [cm 2 /(V·s)] 10 –3 5 μm Mobility [cm 2 /(V·s)] 10 –3 5 μm

10 –4
10 –4
2 μm
2 μm
500 nm
10 –5 1 μm 10 –5 1 μm
500 nm
270 nm 270 nm
Envelope fit Envelope fit
10 –6 10 –6
0 200 400 600 800 0 200 400 600 800
57 K sqrt (V ds /L) (V/cm) 1/2 92 K sqrt (V ds /L) (V/cm) 1/2
V g = –40 V V g = –40 V
(c) (d )
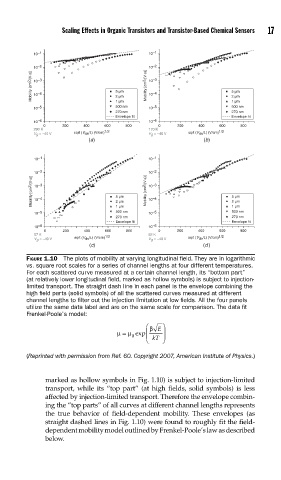
FIGURE 1.10 The plots of mobility at varying longitudinal fi eld. They are in logarithmic
vs. square root scales for a series of channel lengths at four different temperatures.
For each scattered curve measured at a certain channel length, its “bottom part”
(at relatively lower longitudinal fi eld, marked as hollow symbols) is subject to injection-
limited transport. The straight dash line in each panel is the envelope combining the
high fi eld parts (solid symbols) of all the scattered curves measured at different
channel lengths to fi lter out the injection limitation at low fi elds. All the four panels
utilize the same data label and are on the same scale for comparison. The data fi t
Frenkel-Poole’s model:
⎛ β E ⎞
μ = μ exp ⎜ ⎟
0
⎝ kT ⎠
(Reprinted with permission from Ref. 60. Copyright 2007, American Institute of Physics.)

marked as hollow symbols in Fig. 1.10) is subject to injection-limited
transport, while its “top part” (at high fields, solid symbols) is less
affected by injection-limited transport. Therefore the envelope combin-
ing the “top parts” of all curves at different channel lengths represents
the true behavior of field-dependent mobility. These envelopes (as
straight dashed lines in Fig. 1.10) were found to roughly fit the field-
dependent mobility model outlined by Frenkel-Poole’s law as described
below.