Page 307 - Petrophysics 2E

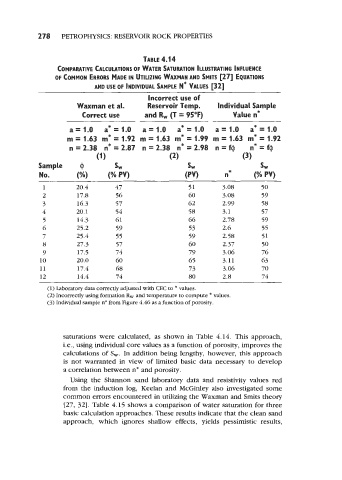
278 PETROPHYSICS: RESERVOIR ROCK PROPERTIES

TABLE 4.14
COMPARATIVE CALCULATIONS OF WATER SATURATION ILLUSTRATING INFLUENCE
OF COMMON ERRORS MADE IN UTILIZING WAXMAN AND SMlTS [27] EQUATIONS
AND USE OF 1NDlVlDUAL SAMPLE N* VALUES 1321
Incorrect use of
Waxman et at. Reservoir Temp. Individual Sample
Correct use and Rw (T = 95°F) Value n*

a= 1.0 a*= 1.0 a= 1.0 a*= 1.0 a= 1.0 a*= 1.0
m = 1.63 m* = 1.92 m = 1.63 m* = 1.99 m = 1.63 m* = 1.92
n = 2.30 n* = 2.07 n = 2.38 n* = 2.90 n = f$ n* = f@
(1) (2) (3)
Sample @ SW sw sw
No. (%) (% PV) (PV) n* (% PV)
1 20.4 47 51 3.08 50
2 17.8 56 60 3.08 59
3 16.3 57 62 2.99 58
4 20.1 54 58 3.1 57
5 14.3 61 66 2.78 59
6 25.2 59 53 2.6 55
7 25.4 55 59 2.58 51
8 27.3 57 60 2.37 50
9 17.5 74 79 3.06 76
10 20.0 60 65 3.11 63
11 17.4 68 73 3.06 70
12 14.4 74 80 2.8 74
(1) Laboratory data correctly adjusted with CEC to * values.
(2) Incorrectly using formation Rw and temperature to compute * values.
(3) Individual sample n* from Figure 4.46 as a function of porosity.

saturations were calculated, as shown in Table 4.14. This approach,
i.e., using individual core values as a function of porosity, improves the
calculations of S,. In addition being lengthy, however, this approach
is not warranted in view of limited basic data necessary to develop
a correlation between n* and porosity.
Using the Shannon sand laboratory data and resistivity values red
from the induction log, Keelan and McGinley also investigated some
common errors encountered in utilizing the Waxman and Smits theory
[27, 321, Table 4.15 shows a comparison of water saturation for three
basic calculation approaches. These results indicate that the clean sand
approach, which ignores shallow effects, yields pessimistic results,