Page 150 - Phase Space Optics Fundamentals and Applications

The Radon-Wigner Transform 131

1000 1000
W = 0 750 W = λ/2
40
40
α = 0°
Irradiance (a.u.) 500 500
α = 0°
750
250

0 250 0
15 15
W = 0 W = λ/2
40
40
α = 0.012°
α = 0.012°
Irradiance (a.u.) 10 5 10 5

0 0
8 8
W = 0 6 W = λ/2
40
40
α = 0.024°
α = 0.024°
Irradiance (a.u.) 4 4
6

0 2 2 0
–4.0 –2.0 0.0 2.0 4.0 –4.0 –2.0 0.0 2.0 4.0
Defocus coefficient: W (μm)
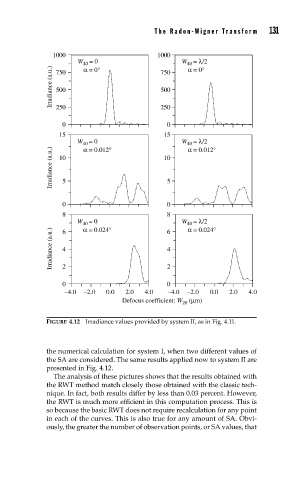
20
FIGURE 4.12 Irradiance values provided by system II, as in Fig. 4.11.

the numerical calculation for system I, when two different values of
the SA are considered. The same results applied now to system II are
presented in Fig. 4.12.
The analysis of these pictures shows that the results obtained with
the RWT method match closely those obtained with the classic tech-
nique. In fact, both results differ by less than 0.03 percent. However,
the RWT is much more efficient in this computation process. This is
so because the basic RWT does not require recalculation for any point
in each of the curves. This is also true for any amount of SA. Obvi-
ously, the greater the number of observation points, or SA values, that