Page 68 - Phase-Locked Loops Design, Simulation, and Applications

MIXED-SIGNAL PLL ANALYSIS Ronald E. Best 48

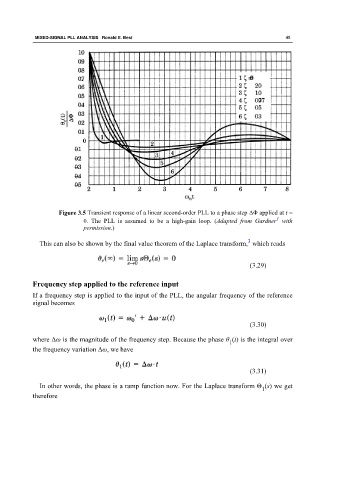
Figure 3.5 Transient response of a linear second-order PLL to a phase step ΔΦ applied at t =
1
0. The PLL is assumed to be a high-gain loop. (Adapted from Gardner with
permission.)

3
This can also be shown by the final value theorem of the Laplace transform, which reads

(3.29)

Frequency step applied to the reference input

If a frequency step is applied to the input of the PLL, the angular frequency of the reference
signal becomes

(3.30)

where Δω is the magnitude of the frequency step. Because the phase θ (t) is the integral over
1
the frequency variation Δω, we have

(3.31)

In other words, the phase is a ramp function now. For the Laplace transform Θ (s) we get
1
therefore