Page 352 - Physical Principles of Sedimentary Basin Analysis

334 Gravity and gravity anomalies

10.10 Gravity from a 2D polygonal body
Most 2D bodies can be quite accurately approximated by a polygon. The gravity at the
origin (0, 0) from a polygonal cross-section is found in a similar way to the gravity from
a 2D body with a rectangular cross-section. It is the integral of line loads that fills the
polygon

z
g = 2G dx dz (10.75)
2
A x + z 2
where dm = dx dz is the mass per unit length in the y-direction, and where the density
is constant inside the area A.Note 10.4 shows that the gravity at the origin then becomes
N
b n r n+1 −1 x n+1 −1 x n

g = 2G ln + a n tan − tan (10.76)
2
a + 1 r n z n+1 z n
n
n=1
when the polygon has N corners with coordinates (x n , z n ) anticlockwise around the
2
2 1/2
perimeter, and where r n = (x + z ) is the distance from the origin to the point n.
n
n
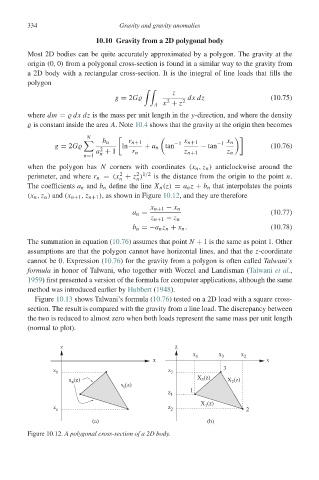
The coefficients a n and b n define the line X n (z) = a n z + b n that interpolates the points
(x n , z n ) and (x n+1 , z n+1 ), as shown in Figure 10.12, and they are therefore
x n+1 − x n
a n = (10.77)
z n+1 − z n
b n =−a n z n + x n . (10.78)
The summation in equation (10.76) assumes that point N + 1 is the same as point 1. Other
assumptions are that the polygon cannot have horizontal lines, and that the z-coordinate
cannot be 0. Expression (10.76) for the gravity from a polygon is often called Talwani’s
formula in honor of Talwani, who together with Worzel and Landisman (Talwani et al.,
1959) first presented a version of the formula for computer applications, although the same
method was introduced earlier by Hubbert (1948).
Figure 10.13 shows Talwani’s formula (10.76) tested on a 2D load with a square cross-
section. The result is compared with the gravity from a line load. The discrepancy between
the two is reduced to almost zero when both loads represent the same mass per unit length
(normal to plot).

z z
x 1 x 3 x 2
x x
z b z 3 3
X (z)
x (z) 3 X (z)
a
x (z) 2
b
z 1 1
X (z)
z a z 2 1 2
(a) (b)
Figure 10.12. A polygonal cross-section of a 2D body.